A bag initially contains 3 red balls and 3 black balls. Whenever a red ball is drawn from the bag, it is put back into the bag together with an extra red ball. Whenever a black ball is drawn from the bag, it is not put back into the bag and no extra balls are added.
Isaac draws \(n\) balls from the bag, one after another, where \(n \in Z ^{*}\), and \(R\) denotes the number of red balls out of the \(n\) balls drawn.
(a) Give two reasons why \(R\) cannot be modelled using a Binomial distribution.
[2]
(b) For \(n=3\), find
(i) \(P (R \geq 1)\),
[2]
(ii) the probability that the first ball drawn is black given that at least 1 of the 3 balls drawn is red.
[3]
(c) For \(n=31\), show that \(P (R=31)=\frac{1}{714}\).
[2]
(d) Isaac wins 100 dollars for each red ball he draws if all the balls he draws from the bag are red, and does not win any money otherwise. What is the maximum amount of money Isaac would win if the probability of all the balls he draws are red exceeds \(0.0001\) ?
[3]
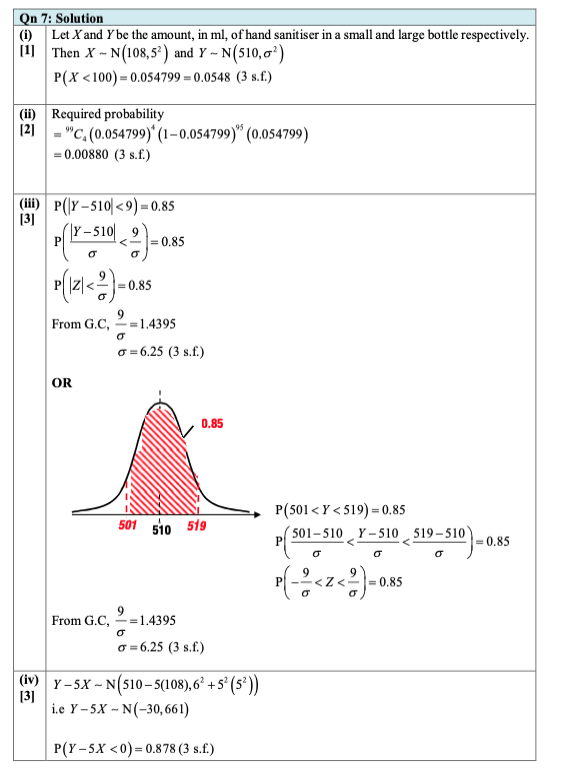
(i) $\mathrm{P}(X<100)=0.054799=0.0548$
(ii) $=0.00880$ (3 s.f.)
(iii) $\sigma=6.25(3$ s.f. $)$