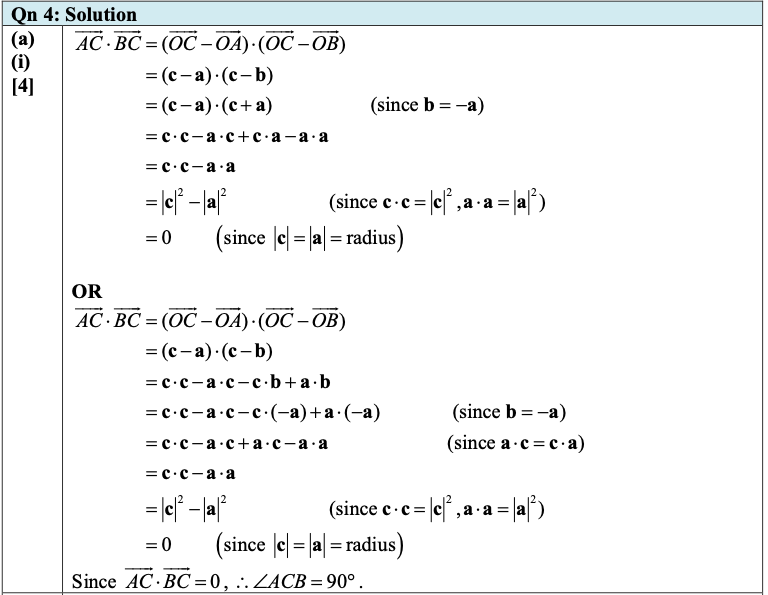
(a)(i)

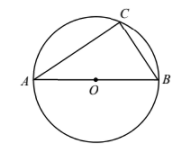
Referred to the origin \(O\), points \(A, B\) and \(C\) have position vectors a, \(b\) and c respectively. The three points lie on a circle with centre \(O\) and diameter \(A B\) (see diagram).

Using a suitable scalar product, show that the angle \(A C B\) is \(90^{\circ}\).

[4]

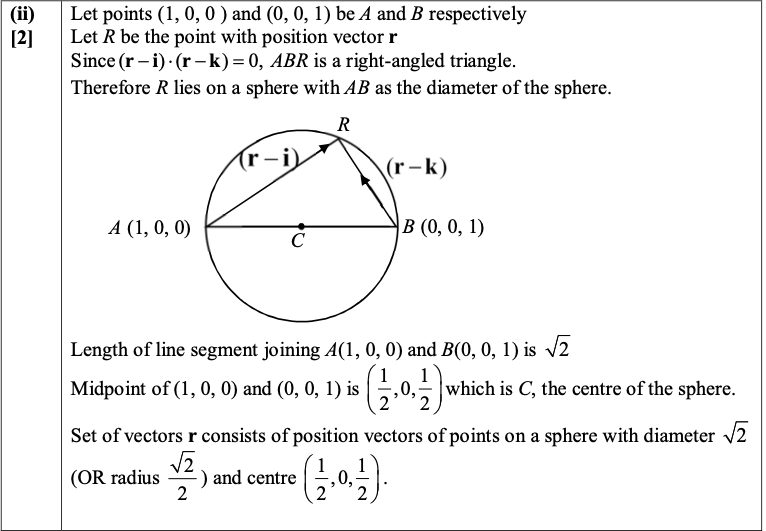
(ii) The variable vector \(r\) satisfies the equation \(( r – i ) \cdot( r – k )=0\). Describe the set of vectors \(r\) geometrically.

[2]

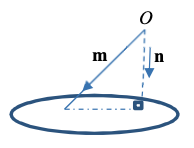
(b) (i) The variable vector \(r\) satisfies the equation \(r \cdot n = m \cdot n\), where \(m\) and \(n\) are constant vectors. Describe the set of vectors \(r\) geometrically. Give the geometrical meaning of \(| m \cdot n |\) if \(n\) is a unit vector.

[2]

(ii) The plane \(\pi\) passes through the points with position vectors \(x i, y j\) and zk where \(x, y\) and \(z\) are non-zero constants. It is given that \(d\) is the perpendicular distance from the origin to \(\pi\). Show, by finding the normal of \(\pi\), or otherwise, that \(\frac{1}{x^{2}}+\frac{1}{y^{2}}+\frac{1}{z^{2}}=\frac{1}{d^{2}}\).

[4]