It is given that \(\ln y=\sqrt{1+8 e ^{x}}\).

(i) Show that \((\ln y) \frac{ d y}{ d x}=4 y e ^{x}\).

[1]

(ii) Show that the value of \(\frac{ d ^{2} y}{ d x^{2}}\) when \(x=0\) is \(\frac{68}{27} e ^{x}\).

[4]

(iii) Hence find the Maclaurin series for \(e ^{\sqrt{1+8 e ^{x}}}\) up to and including the term in \(x^{2}\).

[2]

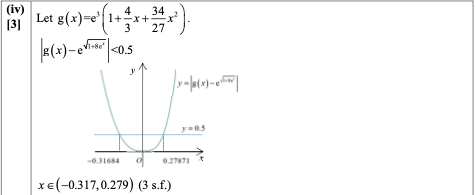
(iv) Denoting the answer found in part (iii) as \(g (x)\), find the set of values of \(x\) for which \(g (x)\) is within \(\pm 0.5\) of the value of \(e ^{\sqrt{1+8 e ^{2}}}\).

[3]