The equations of a plane $p_1$ and a line $l$ are shown below:

Referred to the origin $O$, the position vector of the point $A$ is $2 \mathbf{i}+\mathbf{j}-3 \mathbf{k}$.
(i) Find the coordinates of the foot of perpendicular, $N$, from $A$ to $p_1$.

[4]

(ii) Find the position vector of the point $B$ which is the reflection of $A$ in $p_1$.

[2]

(iii) Hence, or otherwise, find an equation of the line $l^{\prime}$, the reflection of $l$ in $p_1$.

[4]

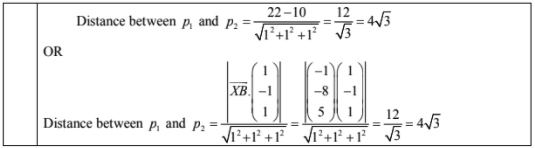
(iv) Another plane, $p_2$, contains $B$ and is parallel to $p_1$. Determine the exact distance between $p_1$ and $p_2$.

[2]