A curve $C$ has parametric equations
$$
x=\sin t, \quad y=\frac{1}{3} \cos t, \text { for }-\pi \leq t \leq \frac{\pi}{4} .
$$
(i) Find the equation of the normal to $C$ at the point $P$ with parameter $t=p$.

[3]

(ii) The normal to $C$ at the point when $t=-\frac{\pi}{4}$ cuts the curve again at point $A$. Find the coordinates of point $A$, correct to 2 decimal places.

[4]

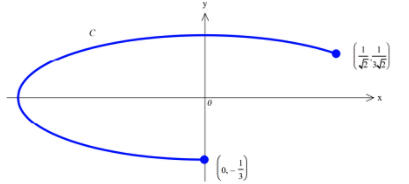
(iii) Sketch the graph of $C$, giving the coordinates of the end points in exact form.

[2]

(iv) Find the area of the region bounded by $C$, the $x$-axis and the lines $x=0$ and $x=\frac{1}{\sqrt{2}}$.

[2]