RI/2021/JC2/Prelim/P1/Q05

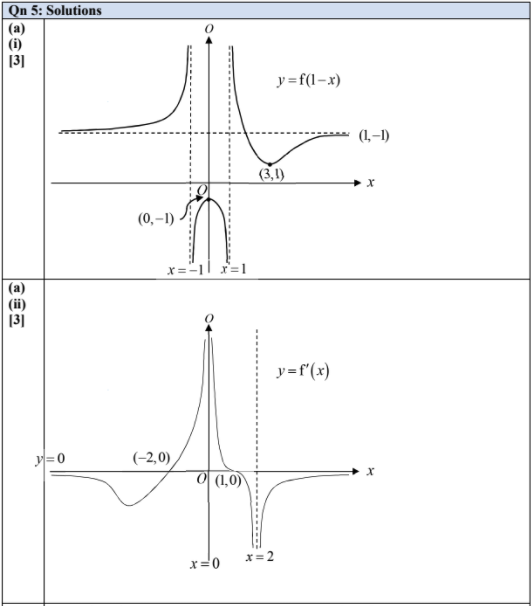
(a) The graph of $y=\mathrm{f}(x)$ is shown below.

On separate diagrams, sketch the following graphs, indicating clearly the key features.
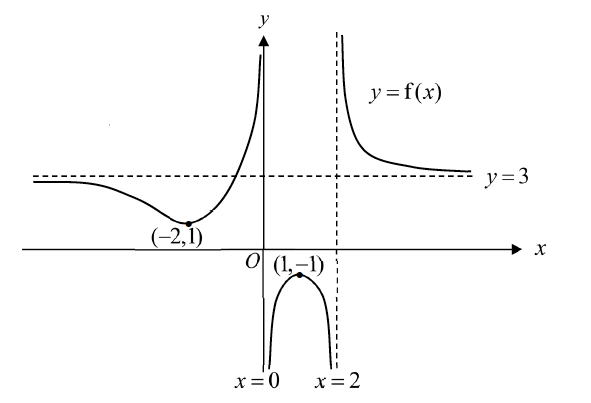
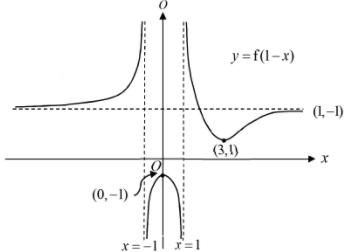
(i) $y=\mathrm{f}(1-x)$,

[3]

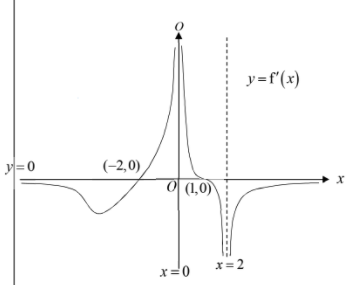
(ii) $y=\mathrm{f}^{\prime}(x)$.

[3]

(b) State a sequence of transformations which transform the graph of $y=\ln \left(1-\frac{x}{2}\right)$ onto the graph of $y=\ln \left(\frac{2}{1-x}\right)$.

[3]

(a)(i)

(a)(ii)

(b) Scale the graph of $y=\ln \left(1-\frac{x}{2}\right)$ parallel to the $x$-axis by factor $\frac{1}{2}$, followed by a reflection about the $x$-axis, followed by a translation of $\ln 2$ units in the positive $y$ direction.

Reflect the graph of $y=\ln \left(1-\frac{x}{2}\right)$ about the $x$-axis, followed by a translation of 1 unit in the negative $x$-direction.