Functions $f$ and $g$ are defined by
$\mathrm{f}: x \mapsto 4 x-2 k \quad$ for $x \in \mathbb{R}$, where $k$ is a constant, $\mathrm{g}: x \mapsto \frac{9}{2-x} \quad$ for $x \in \mathbb{R}, x \neq 2$.
(i) Explain why gf does not exist.
[1]
(ii) Find the range of values of $k$ for which the equation $\mathrm{fg}(x)=x$ has real roots.
[4]
For the rest of the question, let $k=5$.
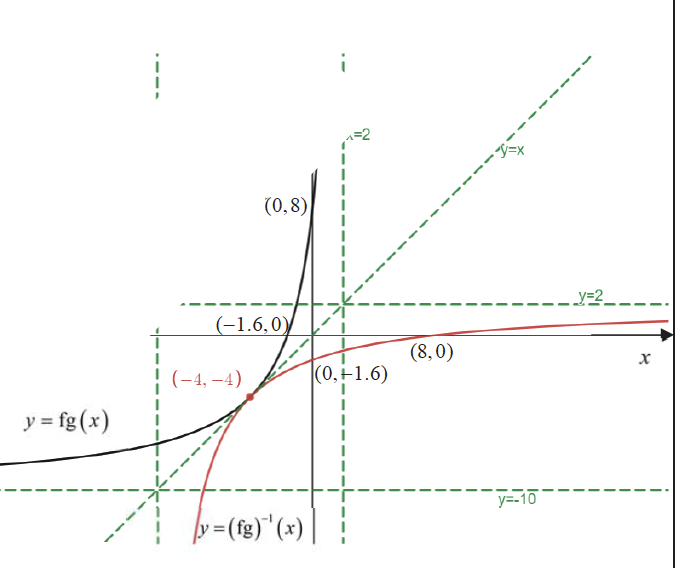
(iii) Sketch the graph of $y=\mathrm{fg}(x)$ for $x<2$. Hence sketch the graph of $y=(\mathrm{fg})^{-1}(x)$ on the same diagram, showing clearly the relationship between the two graphs.
[4]
[Continued]
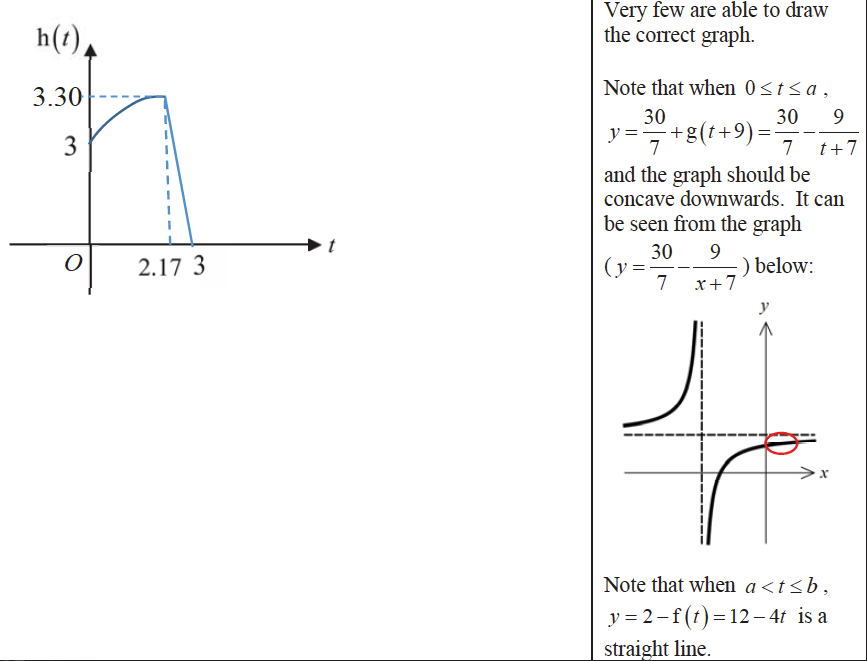
The function h represents the height in metres of an object at time $t$ seconds and is defined for the domain $0 \leq t \leq b$ by
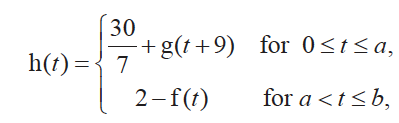
where $a$ and $b$ are constants. At $t=0$, the object was thrown up from 3 metres above the ground level. When $t=a$, the object started to descend and finally reached the ground at $t=b$.
(iv) Find the values of $a$ and $b$.
[2]
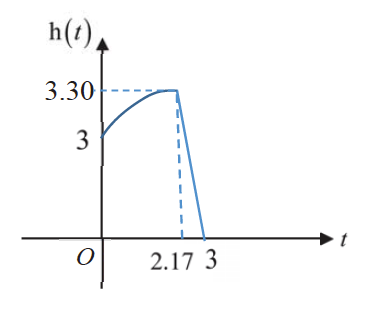
(v) Sketch the graph of $y=\mathrm{h}(t)$ for $0 \leq t \leq b$.
[1]
(ii) $k \leq-7 \text { or } k \geq 5$
(iii)
(iv) $a=2.1738=2.17 \text { (3s.f.) }$ $b=3$
(v)
(i)
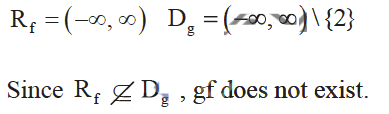
(ii)
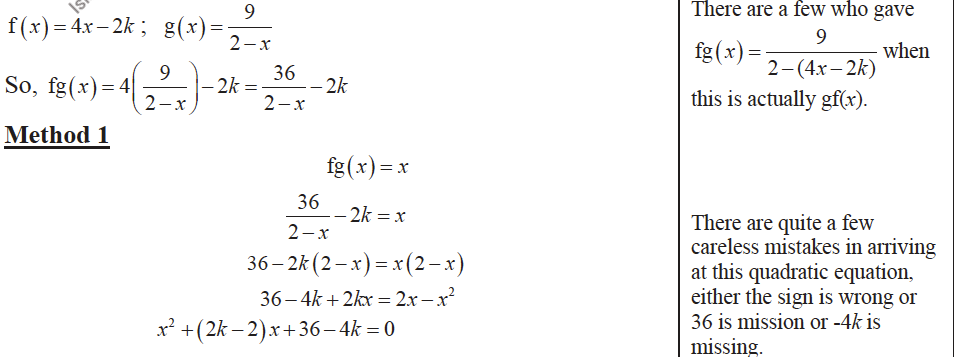
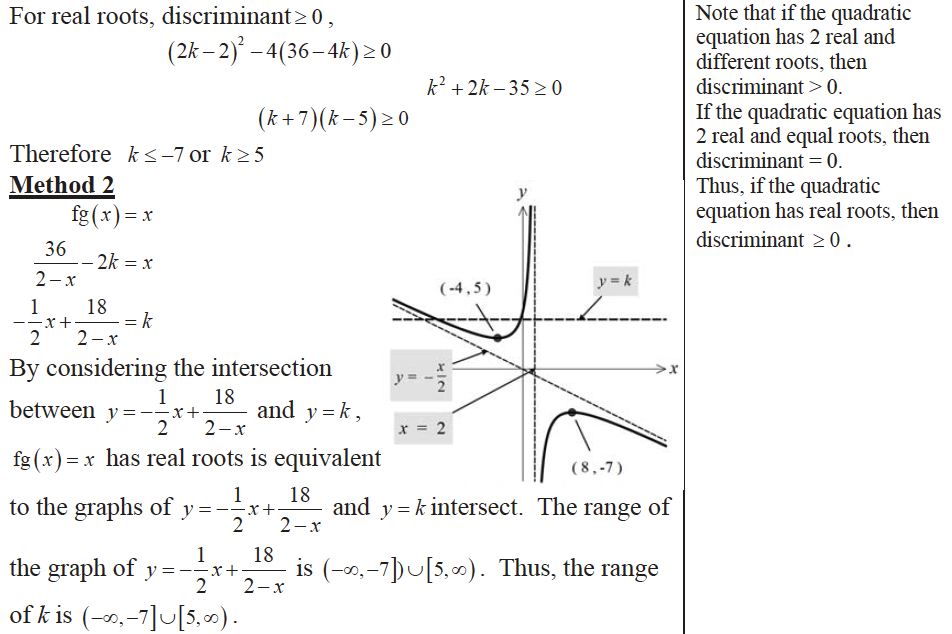
(iii)
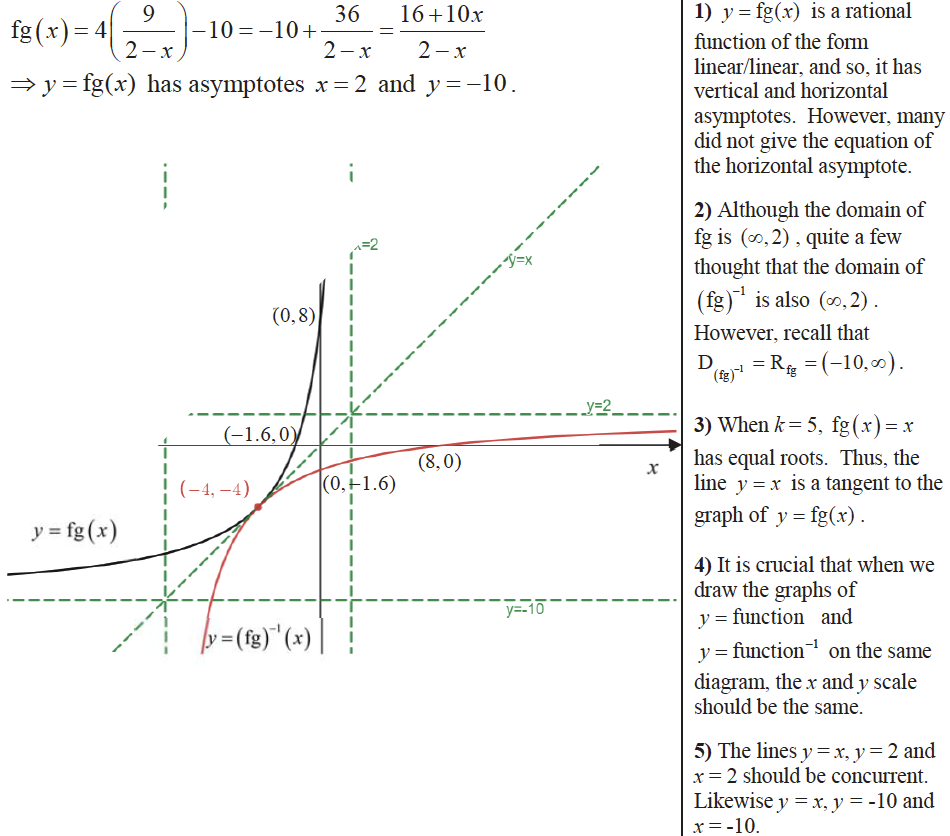
(iv)

(v)