Distances in this question are in metres.
Harry and Tom’s model airplanes are taking off from the horizontal ground, which is the $x-y$ plane. Tom’s airplane takes off after Harry’s. The position of Harry’s airplane $t$ seconds after it takes off is given by $\mathbf{r}=(5 \mathbf{i}+6 \mathbf{j})+t(-4 \mathbf{i}+2 \mathbf{j}+4 \mathbf{k})$. The position of Tom’s airplane $s$ seconds after it takes off is given by $\mathbf{r}=(-39 \mathbf{i}+44 \mathbf{j})+s(4 \mathbf{i}-6 \mathbf{j}+7 \mathbf{k})$.
(i) State the height of Harry’s airplane two seconds after it takes off and find its distance travelled in the two seconds.
[3]
(ii) Find the acute angle between the path of Harry’s airplane and the ground.
[2]
(iii) Show that the paths of the airplanes are perpendicular.
[1]
(iv) Given that the two airplanes collide, find the coordinates of the point of collision. How long after Harry’s airplane takes off does Tom’s airplane take off?
[3]
(v) Find the cartesian equation of the plane in which both paths of the airplanes lie.
[3]
(i) 12m (ii)$\theta=41.8^{\circ}$ (iv) $(-23,20,28)$, 3 seconds (v) $19 x+22 y+8 z=227$
(i)
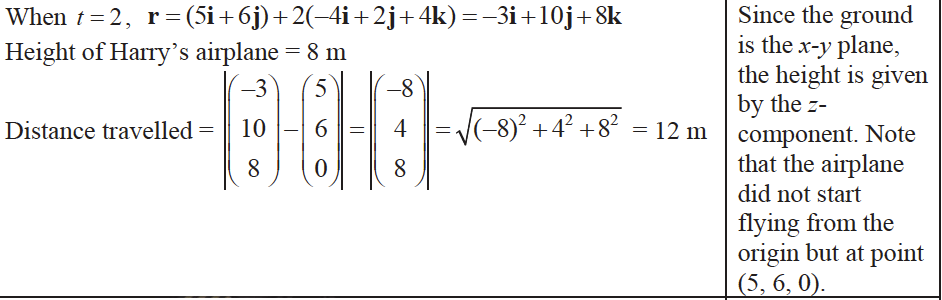
(ii)
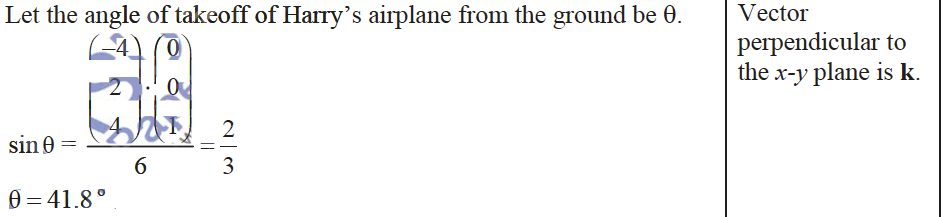
(iii)

(iv) Since the airplanes collide,

(v)

Cartesian equation of the plane is $19 x+22 y+8 z=227$.