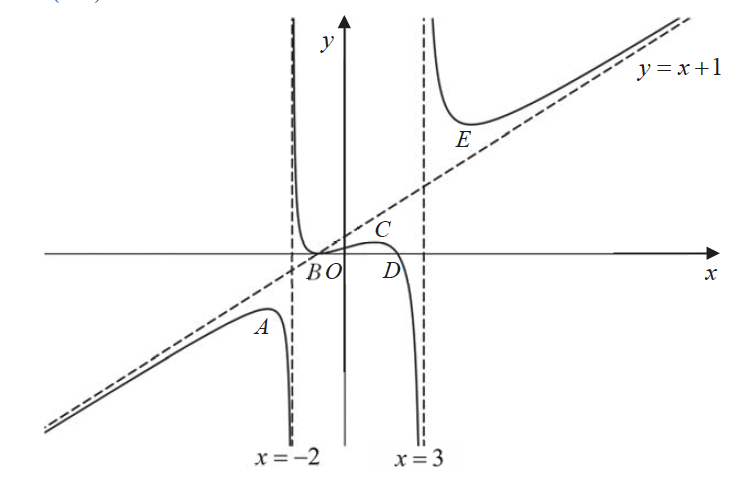
The diagram below shows the graph of $y=\mathrm{f}(x)$ with asymptotes $x=-2, x=3$ and $y=x+1$. The curve intersects the $x$-axis at points $B$ and $D$, and has turning points at points $A, B, C$ and $E$. The coordinates of $A, B, C, D$ and $E$ are $(-3,-3),(-1,0),\left(\frac{3}{2}, \frac{3}{4}\right)$, $(2,0)$ and $(5,8)$ respectively.
(i) By showing clearly the equations of asymptotes and the coordinates of any turning points and the points where the curve crosses the axes, where possible, sketch, on separate diagrams, the graphs of
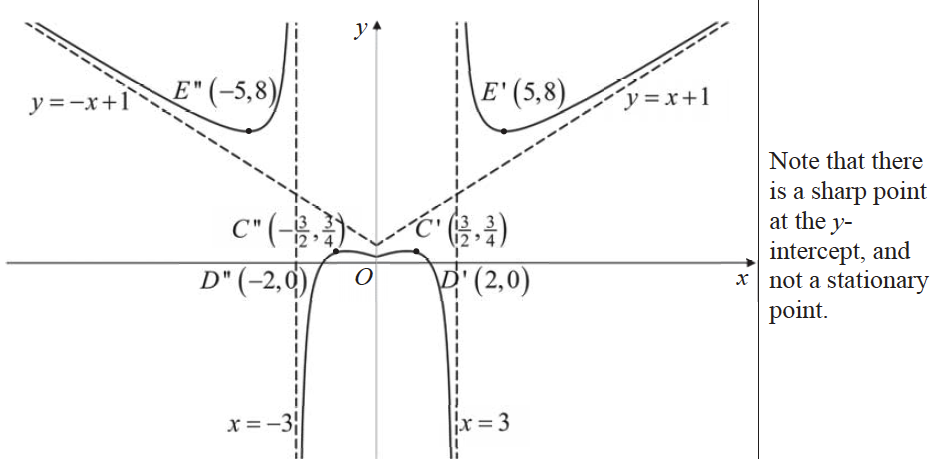
(a) $y=\mathrm{f}(|x|)$
[4]
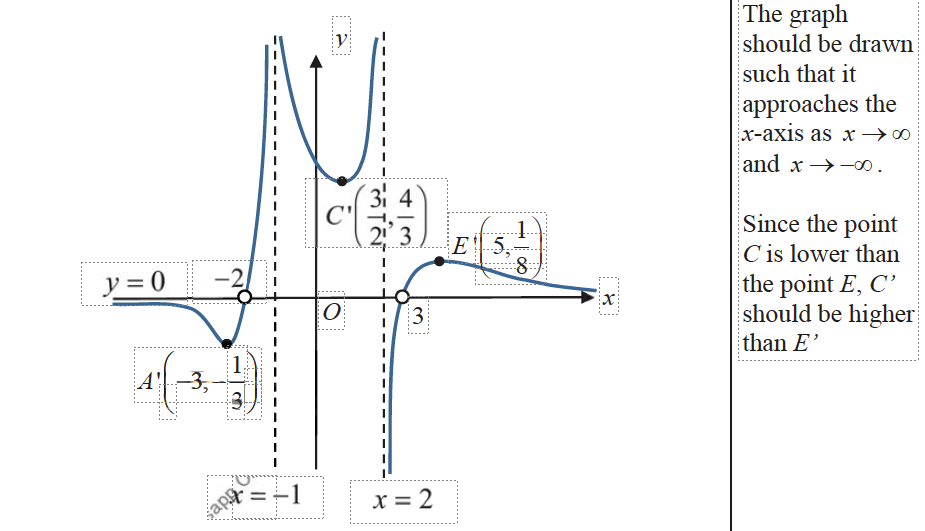
(b) $\quad y=\frac{1}{\mathrm{f}(x)}$.
[4]
(ii) By drawing another suitable graph on the same diagram in part (i)(b), determine the number of solutions to the equation
$$
\frac{x^2}{36}+\frac{1}{16[\mathrm{f}(x)]^2}=1
$$
[2]
8(i)(a)
(b)
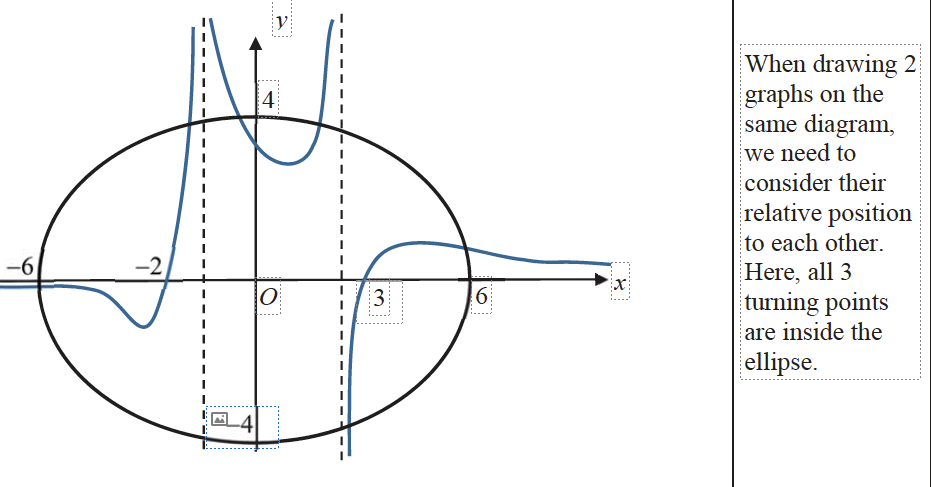
b(ii) 6
(i)(a)

(i)(b)

(ii) $\frac{x^2}{36}+\frac{1}{[f(x)]^2+6}=1$
By drawing $\frac{x^2}{36}+\frac{y^2}{16}=1$ and $y=\frac{1}{f(x)}$, number of solution is 6