NYJC/2021/JC2/Prelim/P1/Q11

In economics, a supply and demand chart is made up of two curves: the supply curve and demand curve. The supply curve is a function that shows how the price of a product, $P$, is related to the quantity, $q$, supplied during a given period of time. The demand curve is a function that shows how the price of the same product is related to the quantity demanded during a given period of time. Due to the nature of the curves, they will intersect at a point which is known as the equilibrium point.

For a particular product, the demand curve is given by the equation $D(q)=75-1.22^q$ where $0 \leq q \leq 21$ and the supply curve is given by the equation $S(q)=2(1.22)^q-1$ using the same domain.
(i) Sketch both curves on thle same diagram. Your sketch should indicate the axial intercepts of both curves.

[3]

(ii) Find the coordinates of the equilibrium point.

[1]

Let $p_e$ be the price of the product at equilibrium point. The area between the demand curve, the line $P=p_e$ and the line $q=0$ is defined as the consumer surplus. In a similar fashion, the area between the supply curve, the line $P=p_e$ and the line $q=0$ is defined as the producer surplus.
(iii) Without using a graphing calculator, determine the consumer surplus and producer surplus, leaving both answer to 2 decimal places.

[4]

A global increase in production lead to a shift of the supply curve to the right. The equation of the new curve is given by $S(q-a)$ where $a$ is a positive constant. The price of the product at the new equilibrium point is denoted by $p_e^*$.

(iv) Show that $\frac{p_e^+1}{p_e+1}=\frac{3}{(1.22)^a+2}$.

[4]

(v) For the case when $a=4$, find the increase in the consumer surplus, leaving your answer to the nearest whole number.

[2]

(i)

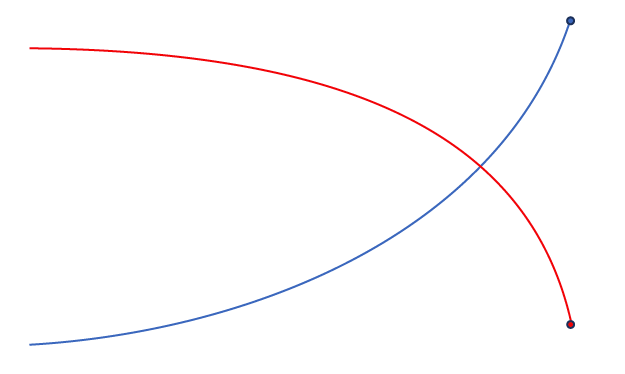
This image has an empty alt attribute; its file name is image-5.png

(ii) Using GC, the coordinates of the equilibrium point is $(16.3,49.7)$.

(iii) Let $q_e$ be the quantity at equilibrium point. Thus
$$
\begin{aligned}
\text { C.S. } &=\int_0^{q_e} D(q) \mathrm{d} q-p_e q_e \\
&=\int_0^{q_e}\left(75-1.22^q\right) \mathrm{d} q-p_e q_e \\
&=\left[75 q-\frac{1.22^q}{\ln (1.22)}\right]_0^{q_e}-p_e q_e \\
&=289.40
\end{aligned}
$$
$$
\begin{aligned}
\text { P.S. } &=p_e q_e-\int_0^{q_e} S(q) \mathrm{d} q \\
&=p_e q_e-\int_0^{q_e}\left(2\left(1.22^q\right)-1\right) \mathrm{d} q \\
&=p_e q_e-\left[\frac{2\left(1.22^q\right)}{\ln (1.22)}-q\right]_0^{q_e}
\end{aligned}
$$

(iv) Let $q_e$ be the quantity at equilibrium point. Thus
$$
\begin{aligned}
\text { C.S. } &=\int_0^{q_e} D(q) \mathrm{d} q-p_e q_e \\
&=\int_0^{q_e}\left(75-1.22^q\right) \mathrm{d} q-p_e q_e \\
&=\left[75 q-\frac{1.22^q}{\ln (1.22)}\right]_0^{q_e}-p_e q_e \\
&=289.40
\end{aligned}
$$
$$
\begin{aligned}
\text { P.S. } &=p_e q_e-\int_0^{q_e} S(q) \mathrm{d} q \\
&=p_e q_e-\int_0^{q_e}\left(2\left(1.22^q\right)-1\right) \mathrm{d} q \\
&=p_e q_e-\left[\frac{2\left(1.22^q\right)}{\ln (1.22)}-q\right]_0^{q_e}
\end{aligned}
$$

(v) $p=75-1.22^q$
$\Rightarrow q=\frac{\ln (75-p)}{\ln (1.22)}$
$p_e^*=\frac{3\left(p_e+1\right)}{(1.22)^4+2}-1=35.0588$
Increase $=\int_{p_c^{:}}^{p_e} \frac{\ln (75-p)}{\ln (1.22)} \mathrm{d} p$
$=255 \quad$ (to nearest whole number)