A designer wishes to create a piece of artwork with painted area of $1200 \mathrm{~cm}^2$ on a rectangular piece of nvas. The painted area measures $x \mathrm{~cm}$ by $y \mathrm{~cm}$ and is surrounded by an unpainted border with top and ttom margins of $3 \mathrm{~cm}$ each, and side margins of $4 \mathrm{~cm}$ each on the canvas, as shown in the diagram below.
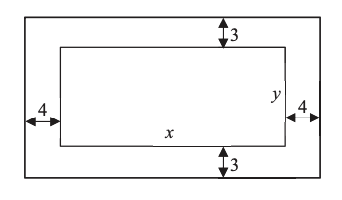
(i) By differentiation, find the dimensions of the canvas with the smallest area.
[6]
(ii) What is the largest possible area of the canvas if $30 \leq x \leq 50$ ?
[2]
At an exhibition, a spotlight illuminates a circular region of radius $\frac{2}{\sqrt{\pi}} \mathrm{cm}$ on the artwork. The area of this circular region then increases at a constant rate of $20 \mathrm{~cm}^2$ per minute.
(iii) Find the rate of change of the radius after 3 minutes.
[4]
(i) $x$ = 48 $cm$, $y$ = 36 $cm$
(ii) s $1748 \mathrm{~cm}^2$
(iii) $0.705 \mathrm{~cm} / \mathrm{min}$
(i)

$x y=1200 \Rightarrow y=\frac{1200}{x}$
Let $A$ be the total area of the canivas.
To minimize $A=(x+8)(y+6)$
$=(x+8)\left(\frac{1200}{n}+6\right)$
$-=1200+6 x+\frac{9600}{x}+48 $
$=6 x^2+\frac{9600}{x}+1248 $
$\frac{\mathrm{d} A}{\mathrm{~d} x} =6-\frac{9600}{x^2} $
$\frac{\mathrm{d} A}{\mathrm{~d} x} =0 \quad \Rightarrow \quad x^2=1600 $
$x =40 \quad(\because x>0) $
$y =30 \quad$
$\frac{\mathrm{d}^2 A}{\mathrm{~d} x^2}=\frac{19200}{x^3}>0$ since $x>0$
Hence $A$ is minimum when $x=48 \mathrm{~cm}$ and $y=36 \mathrm{~cm}$

(ii) Graph of $A=6 x+\frac{9600}{x}+1248$
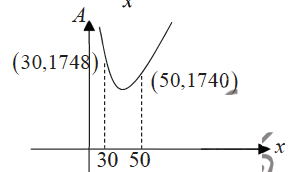
From graph, largest possible area of the canvas is $1748 \mathrm{~cm}^2$ when $x=30 \mathrm{~cm}$.
(iii)
$$
\begin{aligned}
A &=\pi r^2 \
\frac{\mathrm{d} A}{\mathrm{~d} t} &=2 \pi r \frac{\mathrm{d} r}{\mathrm{~d} t} \cdots(*)
\end{aligned}
$$
When $t=0, A=\pi\left(\frac{2}{\sqrt{\pi}}\right)^2=4$
When $t=3, A=4+3 \times 20=64$
Hence $64=\pi r^2 \quad \Rightarrow \quad r=\frac{8}{\sqrt{\pi}}$
Sub $\frac{\mathrm{d} A}{\mathrm{~d} t}=20, r=\frac{8}{\sqrt{\pi}} \operatorname{int} \theta(\gamma)$ :
$$
\begin{array}{l}
20=2 \pi \frac{8}{\sqrt{\pi}} \cdot \frac{\mathrm{d} r}{\mathrm{~d} t} \
\frac{\mathrm{d} r}{\mathrm{~d} t}=\mathbf{0 . 7 0 5} \text { (3.s.f.) }
\end{array}
$$
When $t=B$, rate of change of radius is $0.705 \mathrm{~cm} / \mathrm{min}$