A curve $C$ has parametric equations
$$
x=3 t^2, \quad y=a\left(t^3+1\right),
$$
where $a$ is a positive constant.
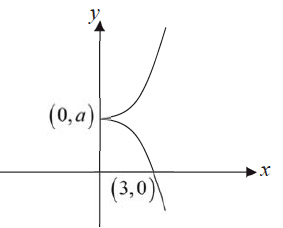
(i) Sketch $C$, giving the coordinates of any point(s) where the curve meets the axes.
[2]
The tangent to $C$ at point $A(3,2 a)$ makes an angle of $\frac{\pi}{3}$ with the positive $x$-axis.
(ii) Show that $a=2 \sqrt{3}$, and find the equation of the tangent to $C$ at $A$ in the form $y=m x+c$, where $m$ and $c$ are constants to be determined.
[5]
(iii) The tangent and the normal to $C$ at $A$ meet the $x$-axis at $T$ and $N$ respectively. Find the exact area of triangle $A T N$.
[3]
(i)
(ii) $y=\sqrt{3} x+\sqrt{3}$
(iii) $=32 \sqrt{3}$ sq. units
(i) When $x=0$,
$3 t^2=0 \Rightarrow t=0$
$y=a$
When $y=0$,
$a\left(t^3+1\right) \Rightarrow t=-1$
$x=3$

$x=3 t^2 \quad y_j=a\left(\rho^3+1\right)$
$\frac{\mathrm{d} x}{\mathrm{~d} t}=6 t \quad \frac{\mathrm{d} y}{\mathrm{~d} t}=3 a t^2$
$\frac{\mathrm{d} y}{\mathrm{~d} x}=\frac{\mathrm{d} y}{\mathrm{~d} t} / \frac{\mathrm{d} x}{\mathrm{~d} t}=\frac{1}{2} a t$
At $A(3,2 a), 2 a b a\left(t^3+1\right)$
$2=t^3+1$
$t^3=1$
$t=1$
Hence $\frac{\mathrm{d} y}{\mathrm{~d} x}=\frac{1}{2} a$
$\frac{1}{2} a=\tan \frac{\pi}{3}=\sqrt{3}$
Hence $a=2 \sqrt{3}$
Equation of the tangent at $A$,
$y-2 a =\frac{1}{2} a(x-3)
y-4 \sqrt{3} =\sqrt{3}(x-3)
y =\sqrt{3} x+\sqrt{3}$
(iii) Equation of the normal at $A$,
$y-4 \sqrt{3} =-\frac{1}{\sqrt{3}}(x-3) $
$y =-\frac{1}{\sqrt{3}} x+5 \sqrt{3}$
When $y=0$,
$0=\sqrt{3} x+\sqrt{3} \Rightarrow x=-1 \quad T(-1,0)$
$0=-\frac{1}{\sqrt{3}} x+5 \sqrt{3} \Rightarrow x=15 \quad \mathbb{N}(15,0)$
Hence area of triangle $A T N=\frac{1}{2}(15-(5+1))(4 \sqrt{3})$ $=32 \sqrt{3}$ sq. units