(i) Amanda wants to make a mask holder. To do so, she cuts out 4 identical equilateral triangles of sides $1 \mathrm{~cm}$ and a rectangular strip $\frac{x-1}{16} \mathrm{~cm}$ by $\frac{2 y-1}{4} \mathrm{~cm}$ from a rectangle of sides $x \mathrm{~cm}$ by $y \mathrm{~cm}$ (see Diagram A). The rectangular strip has an area of $5.5 \mathrm{~cm}^2$.

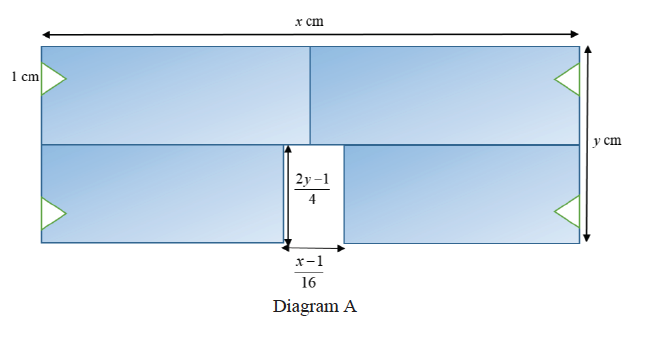
Show that $A$, the area of the mask holder is given by
$A=\frac{176 x}{x-1}+\frac{x}{2}-\sqrt{3}-\frac{11}{2}$
Using differentiation, find the exact value of $x$ such that area of the mask holder is a minimum. Hence determine the minimum area of the mask holder.

[9]

(ii) The area of the rectangular strip is kept at $5.5 \mathrm{~cm}^2$. Beth suggests that if the 4 identical triangle cut-outs are isosceles instead, the area of the mask holder could be made smaller as compared to the area found in part (i)(b).

For each of the triangles, let $\theta$ be the angle between two edges of length $1 \mathrm{~cm}$ each (see diagram B). Determine if Beth’s suggestion is correct.

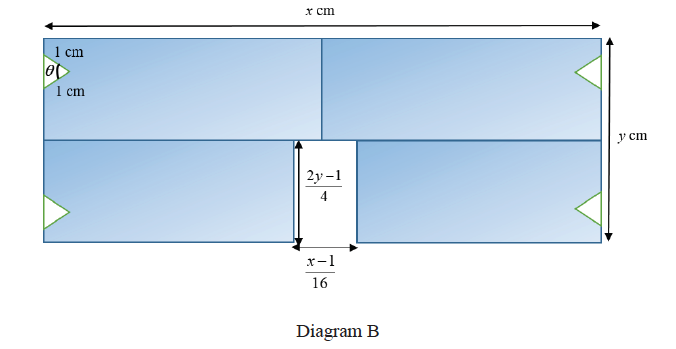
[2]