The diagram below shows the graph of $y=f(x)$. There are two vertical asymptotes with equations $x=-a$ and $x=a$, where $a$ is a positive real constant, $a>1$. There is an oblique asymptote with equation $y=x+a$. The points $A, B$ and $C$ have coordinates $(-2,0),(0,-2)$ and $(1.5,0)$ respectively, where $B$ is also a maximum turning point.

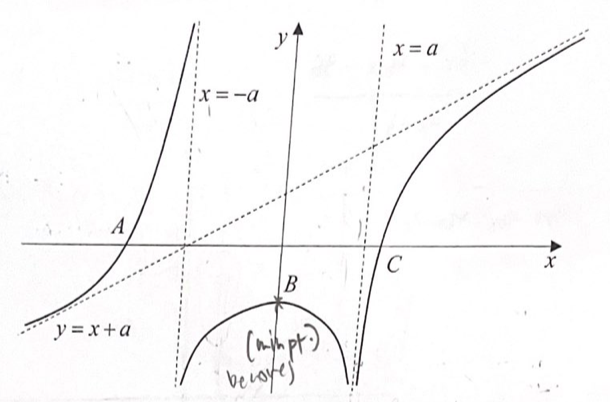
Sketch the following curves and state the equations of the asymptotes, the coordinates of the turning points and of points where the curve crosses the axes, if any. Leave your answers in terms of $a$ where necessary.

(i) $y=\frac{1}{f(x)}$,

[3]

(ii) $y=\mathrm{f}(1-2 x)$.

[3]