Referred to the origin $O$, the points $A, B$ and $C$ have position vectors $4 \mathbf{i}-2 \mathbf{j}$, $\alpha \mathbf{i}-\mathbf{j}+2 \mathbf{k}$ and $-\mathbf{i}-7 \mathbf{j}+\beta \mathbf{k}$ respectively, where $\alpha$ and $\beta$ are constants.
(i) Given that $A, B$ and $C$ are collinear, show that $\alpha=5$, and find the value of $\beta$.
[3]
The plane $\pi$ contains the line $L$, which has equation $\mathbf{r}=2 \mathbf{i}+3 \mathbf{j}+\mu(2 \mathbf{i}-\mathbf{j}+\mathbf{k})$. The plane $\pi$ is also parallel to the line that passes through the points $A$ and $B$.
(ii) Find the shortest distance from point $A$ to the line $L$.
[2]
(iii) Show that the cartesian equation of the plane $\pi$ is $x+y-z=5$.
[2]
(iv) Find the position vector of the foot of the perpendicular from point $A$ to the plane $\pi$.
[3]
(v) Hence find the reflection of the line that passes through points $A$ and $B$ about the plane $\pi$.
[2
(i) $\beta=-10$
(ii) Distance from $A$ to $L$ = $\sqrt{\frac{31}{2}}$
(iv)
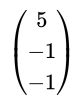
(v)
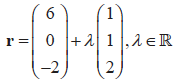
(i)
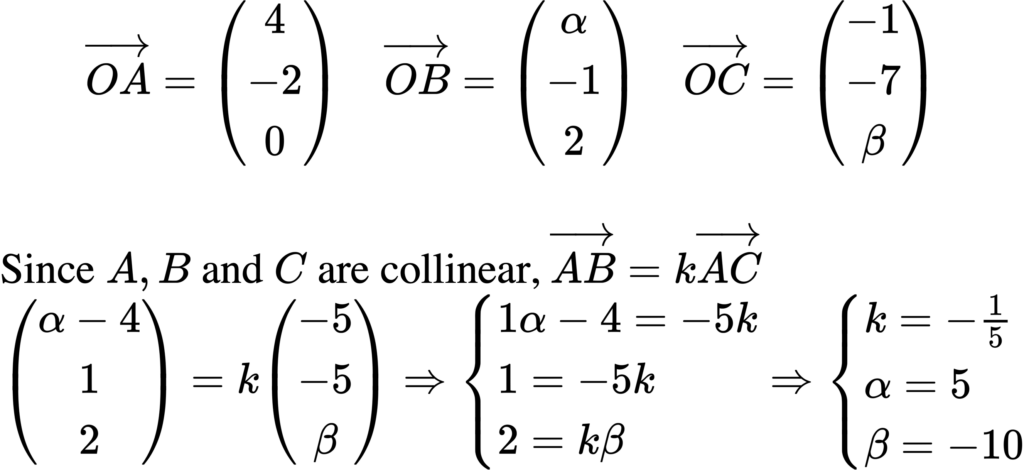
$\beta=-10$
(ii)


(iii)
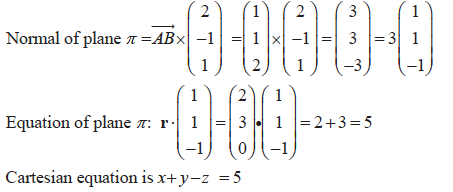
(iv)

(v)
