(a) $2^7\left(2^{n-5}-1\right)+\frac{(n+1)}{6}(n+2)(2 n+3)-91-\frac{(n-5)(8+n)}{2}$

(b)(i) $A=-\frac{1}{2}$.

(ii) As $n \rightarrow \infty, \frac{1}{n} \rightarrow 0, \frac{1}{n+1} \rightarrow 0$, therefore $\sum_{r=2}^{\infty} \frac{1}{r^2-1}$ converges. $\sum_{x=2}^{\infty} \frac{1}{r^2-1}=\frac{3}{4}$

(iii) See worked solution

(a)

$\sum_{r=7}^{n=7}\left(2^r+r^2-2\right)$
$=\sum_{r=1}^{n+1}\left(2^r\right)+\sum_{r=7}^{n+1}\left(r^2\right)-\sum_{r=7}^{n+1}(r)$
$=\frac{2^7\left(2^{n-5}-1\right)}{2-1}+\sum_{r=1}^{n+1}\left(r^2\right)-\sum_{r=1}^6\left(r^2\right)-\left(\frac{n-5}{2}\right)(7+n+1)$
$=2^7\left(2^{n-5}-1\right)+\frac{(n+1)}{6}(n+2)(2 n+3)-\left(\frac{6}{6}\right)(7)(13)-\left(\frac{n-5}{2}\right)(8+n)$
$=2^7\left(2^{n-5}-1\right)+\frac{(n+1)}{6}(n+2)(2 n+3)-91-\frac{(n-5)(8+n)}{2}$

 

(b)(i)

Using partial fractions,
$\frac{1}{r^2-1}=\frac{1}{2}\left(\frac{1}{r-1}-\frac{1}{r+1}\right) $
$\sum_{r=2}^n \frac{1}{r^2-1}=\frac{1}{2} \sum_{r=2}^n\left(\frac{1}{r-1}-\frac{1}{r+1}\right)$

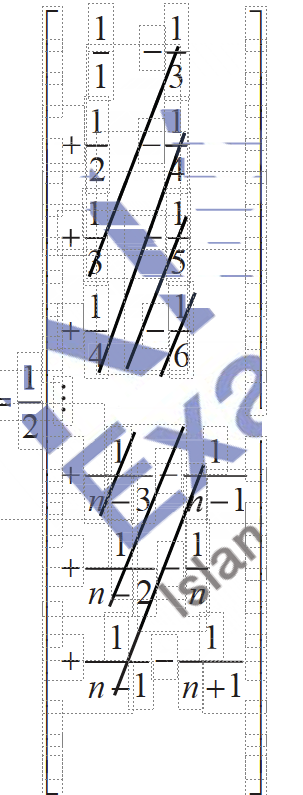
$=\frac{1}{2}\left(\frac{3}{2}-\frac{1}{n}-\frac{1}{n+1}\right)$

$=\frac{3}{4}+\frac{-\frac{1}{2}}{n}+\frac{-\frac{1}{2}}{n+1}$

$\therefore A=-\frac{1}{2}$

(ii)

As $n \rightarrow \infty, \frac{1}{n} \rightarrow 0, \frac{1}{n+1} \rightarrow 0$, therefore $\sum_{r=2}^{\infty} \frac{1}{r^2-1}$ converges. $\sum_{x=2}^{\infty} \frac{1}{r^2-1}=\frac{3}{4}$

(iii)$\frac{2}{2^2}+\frac{2}{3^2}+\frac{2}{4^2}+\ldots=\sum_{r=2}^{\infty} \frac{2}{r^2}$
Since $r^2-1 < \frac{2}{r^2},$
$\sum_{r=2}^{\infty} \frac{2}{r^2-1}>\sum_{r=2}^{\infty} \frac{2}{r^2} $
$\sum_{r=2}^{\infty} \frac{2}{r^2}<2\left(\frac{3}{4}\right) $
$\therefore \frac{2}{2^2}+\frac{2}{3^2}+\frac{2}{4^2}+\ldots<\frac{3}{2}(\text { shown })$