ACJC/2021/JC1/Promo/P1/Q07

The functions $f$ and $g$ are defined by
$\mathrm{f}: x \mapsto \frac{1}{\left|1-x^2\right|}, x \in \mathbb{R},-2 \leq x<-1,$
g: $x \mapsto-(x-2)^2+k, x \in \mathbb{R}, \quad x \geq 0$ where $k$ is a constant.

(i) Sketch on the same diagram the graphs of
(a) $y=\mathrm{f}(x)$
(b) $y=\mathrm{f}^{-1}(x)$
(c) $y=\mathrm{f}^{-1} \mathrm{f}(x)$

stating the equations of any asymptotes and the coordinates of any endpoints.

[3]

(ii) Find $\mathrm{f}^{-1}$ and state the domain of $\mathrm{f}^{-1}$.

[3]

(iii) Show that the composite function gf exists and find its range.

[2]

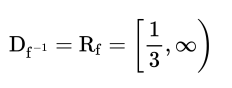
(i)

(ii)

(ii) Considering the interval $-2 \leq x<-1, \frac{1}{\left|1-x^2\right|}=-\frac{1}{1-x^2}$

$y=-\frac{1}{1-x^2}$

$y=\frac{1}{x^2-1}$

$y x^2-y=1$

$x^2=\frac{1+y}{y}$

$x=\pm \sqrt{\frac{1+y}{y}}$

$x=-\sqrt{\frac{1+y}{y}}($ since $-2 \leq x<-1)$

$\mathrm{f}^{-1}(x)=-\sqrt{\frac{1+x}{x}}=-\sqrt{\frac{1}{x}+1}$

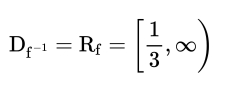
(iii) Since $R_f=\left[\frac{1}{3}, \infty\right) \subseteq[0, \infty)=D_g$
Hence gf exists.
${[-2,-1) \stackrel{f}{\longrightarrow}\left[\frac{1}{3}, \infty\right) \stackrel{g}{\longrightarrow}(-\infty, k]} $
$\mathrm{R}_{\mathrm{gf}}=\left(-\infty, k\right]$