$x<-2$ or $x>1$

$-\frac{1}{2}<x<0$ or $0<x<1$

$\frac{x+3}{x^2+x-2}>-1 $
$\frac{x+3}{x^2+x-2}+1>0 $
$\frac{x^2+2 x+1}{x^2+x-2}>0 $
$\frac{(x+1)^2}{(x+2)(x-1)} \geq 0$
Since $(x+1)^2 \geq 0$ for $x \in \mathbb{R},(x+2)(x-1)>0$. $\therefore x<-2$ or $x>1$.

$\therefore x<-2$ or $x>1$

$\frac{x+3 x^2}{1+x-2 x^2}>=1$
$\frac{\frac{x+3 x^2}{x^2}}{\frac{1+x-2 x^2}{x^2}}>-1$
$\frac{\frac{1}{x}+3}{\left(\frac{1}{x}\right)^2+\left(\frac{1}{x}\right)-2}>-1$

Replace $x$ by $\frac{1}{x}$
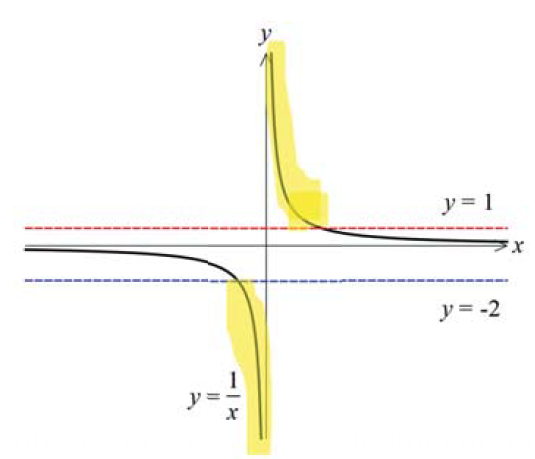
$\frac{1}{x}<-2$ or $\frac{1}{x}>1$
$\therefore-\frac{1}{2}<x<0$ or $0<x<1$