10 A curve $C$ has equation $y=a x+b+\frac{a+2 b}{x-1}$, where $a$ and $b$ are real constants such that $a>0, b \neq-\frac{1}{2} a$ and $x \neq 1$.
(a) Given that $C$ has no stationary points, use differentiation to find the relationship between $a$ and $b$.
[3]
It is now given that $b=-2 a$.
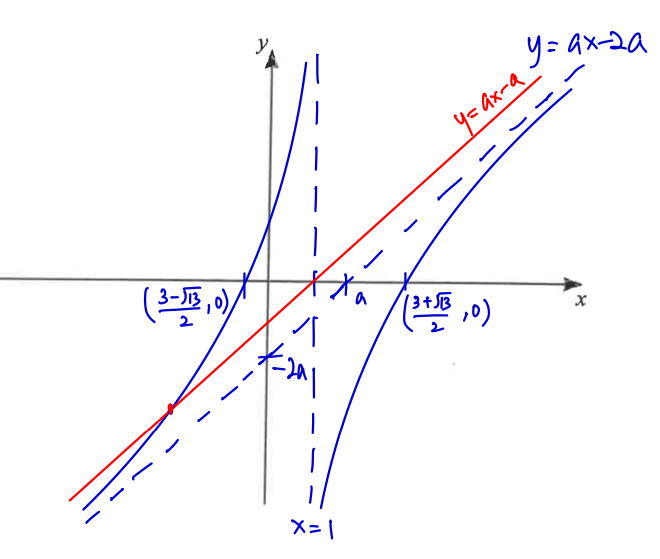
(b) Sketch $C$ on the axes on page 19 stating the equations of any asymptotes and the coordinates of the points where $C$ crosses the axes.
[4]
(c) On the same axes, sketch the graph of $y=a x-a$.
[1]
(d) Hence solve the inequality $x-2-\frac{3}{x-1} \leqslant x-1$.
[2]
(a) $a<-2 b $
(b) (c)
(d) $ x \leq-2$ or $x>1$
(a) $\frac{d y}{d x}=a-(a+2 b)(x-1)^{-2}$
$\frac{d y}{d x}=0 \quad a=\frac{a+2 b}{(x-1)^2}$
$(x-1)^2=\frac{a+2 b}{a}$
$x^2-2 x+1-\frac{a+2 b}{a}=0$
$\therefore $ No turning point
$b^2-4 a c<0$
$4-4(1)\left(1-\frac{a+2 b}{a}\right)<0$
$1-1+\frac{a+2 b}{a}<0$
$a+2 b<0$
$a<-2 b$
(b) $y=a x-2 a-\frac{3 a}{x-1}$
When $x=0 \quad y=-2 a+3 a$
when $y=0 \quad a x-2 a=\frac{3 a}{x-1}$
$$
\begin{aligned}
&(x-2)(x-1)=3 \\
& x^2-3 x-1=0 \\
& x: \frac{3 \pm \sqrt{9-4(1)(-1)}}{2} \\
& x: \frac{3 \pm \sqrt{13}}{2} \\
\text { asymptotes } x=1, y=a x-2 a
\end{aligned}
$$
$\therefore b=-2 a$, carve has no stationary pant

(c) See graph
(d) $$
\begin{aligned}
a\left(x-2-\frac{3}{x-1}\right) & \leqslant a(x-1) \quad \because a>0 \\
a x-2 a-\frac{3 a}{x-1} & \leqslant a x-a \\
-a-\frac{3 a}{x-1} & \leqslant 0 \\
1-\frac{3}{x-1} & \leqslant 0
\end{aligned}
$$
From graph: $x \leqslant-2$ or $x>1$