Question
Answer Key
Worked Solution
9758/2021/P2/Q06
A biased 5 -sided spinner gives the scores $1,2,3,4$ and 5 with the probabilities shown in the table where $p$ and $q$ are constants.
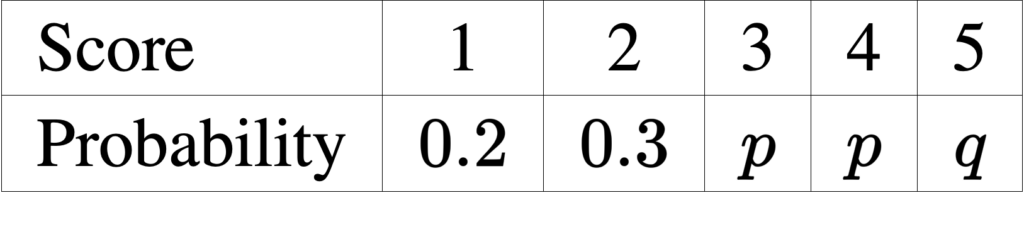
Given that the variance of the score is $1.61$, calculate the mean score.
[7]
$p=0.2, q=0.1$, mean $=2.7$
[Maximum marks: 7 marks]
Let $X$ be the score of the spinner.
$$
\begin{array}{l}
0.2+0.3+p+p+q=1 \Rightarrow q=0.5-2 p \\
E(X)=1(0.2)+2(0.3)+3(p)+4(p)+5(q) \\
E(X)=0.8+7 p+5(0.5-2 p) \\
E(X)=3.3-3 p \\
E\left(X^2\right)=1^2(0.2)+2^2(0.3)+3^2(p)+4^2(p)+5^2(q) \\
E\left(X^2\right)=1.4+25 p+25(0.5-2 p) \\
E\left(X^2\right)=13.9-25 p \\
\operatorname{Var}(X)=1.61 \\
13.9-25 p-(3.3-3 p)^2=1.61
\end{array}
$$
Using $\mathrm{GC}, p=0.2$.
$$
q=0.5-2(0.2)=0.1
$$
Mean score $=3.3 .-2(0.2)=2.7$