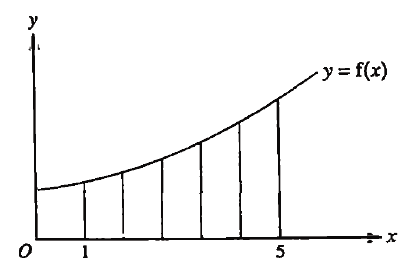
The diagram shows a sketch of the curve $y=f(x)$. The region under the curve between $x=1$ and $x=5$, shown shaded in the diagram, is $A$. This region is split into 5 vertical strips of equal width, $h$.
[2]
(a) State the value of $h$ and show, using a sketch, that $\sum_{n=0}^4(\mathrm{f}(1+n h)) h$ is less than the area of $A$.
[2]
(b) Find a similar expression that is greater than the area of $A$.
[1]
You are now given that $\mathrm{f}(x)=\frac{1}{20} x^2+1$
(c) Use the expression given in part (a) and your expression from part (b) to find lower and upper bounds for the area of $A$.
[2]
(d) Sketch the graph of a function $y=\mathrm{g}(x)$, between $x=1$ and $x=5$, for which the area between the curve, the $x$-axis and the lines $x=1$ and $x=5$ is less than $\sum_{n=0}^4(\mathrm{~g}(1+n h)) h$.
[1]
[4]
$h=0.8 ; 5.608<A<6.568$
(a)
$h=\frac{5-1}{5}=0.8$
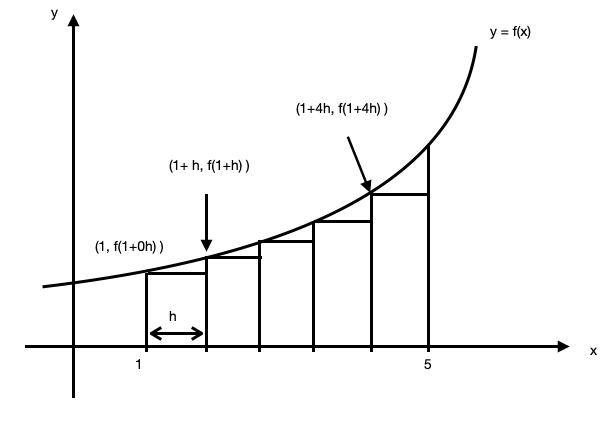
From the graph, we can observe that each rectangle has a constant width of $h$ and the height of each rectangle is given by the $y$ coordinate. Also note that the same of rectangles here is an underestimation of the area under the curve $y=f(x)$ from $x=1$ to $x=5$.
Sum of rectangles $=h \times f(1+0 h)+h \times f(1+h)+\ldots+h \times f(1+4 h)$
Sum of rectangles $=\sum_{n=0}^4 h \times f(1+n h)$
Sum of rectangles $=\sum_{n=0}^4[f(1+n h)] h$
Actual area under the graph $=A$
Thus, $\sum_{n=0}^4[f(1+n h)] h<A$
(b)
Required expression: $\sum_{n=1}^5[f(1+n h)] h$
Explanation (if you are interested): The rectangles in (a) touches the curve on the left corners while the rectangles in (b) is meant to touch the curve on the right corners. Thus, we simply need to “shift” one term to the right.
(c)
$$
\begin{array}{l}
h=1 \text { and } f(x)=\frac{1}{20} x^2+1 \\
\sum_{n=0}^4[f(1+n h)] h \\
=\sum_{n=0}^4\left[\frac{1}{20}(1+0.8 n)^2+1\right](0.8) \\
=5.608 \text { using GC. } \\
\sum_{n=1}^5[f(1+n h)] h \\
=\sum_{n=1}^5\left[\frac{1}{20}(1+0.8 n)^2+1\right](0.8) \\
=6.568 \text { using GC. } \\
\therefore \quad 5.608 \leq A \leq 6.568
\end{array}
$$
(d)
Let $g(x)=5-x$.
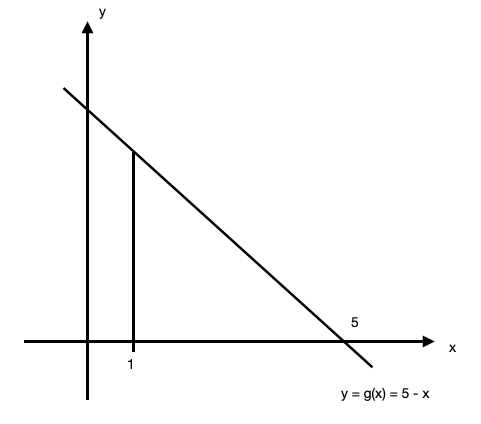
Note: There are many possible answers here, a decreasing function should be good. My choice came up to me as the easiest. I will verify it.
$$
\begin{array}{l}
\int_1^5(5-x) d x=8 \\
\sum_{n=0}^4[5-(1+0.8 x)](0.8)=14.6
\end{array}
$$