Civil engineers design bridges to span over expressways. The diagram below represents a bridge over an expressway. $P S$.
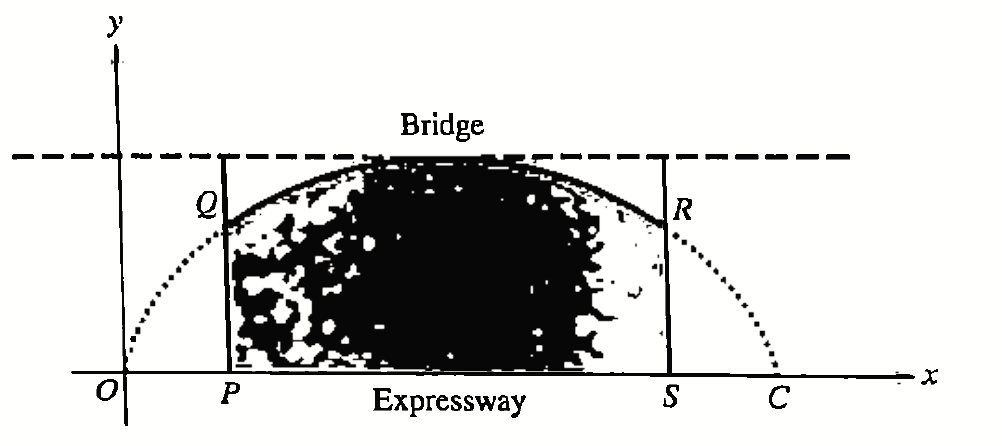
In the diagram, $P Q$ and $S R$ are parallel to the $y$-axis, and $P Q=S R$. The arch of the bridge, $Q R$, forms part of the curve $O Q R C$ with parametric equations
$$
x=a(\theta-\sin \theta), \quad y=a(1-\cos \theta), \quad \text { for } 0 \leqslant \theta \leqslant 2 \pi,
$$
where $a$ is a positive constant. The units of $x$ and $y$ are metres.
At the point $Q, \theta=\beta$ and at the point $R, \theta=2 \pi-\beta$.
(a) Find, in terms of $a$ and $\beta$, the distance $P S$.
[2]
(b) Show that the area of the shaded region on the diagram, representing the area under the bridge, is
$$
\frac{1}{2} a^2(6 \pi-6 \beta+8 \sin \beta-\sin 2 \beta) \text {. }
$$
[6]
(c) It is given that the area under the bridge, in square metres, is $7.8159 a^2$. Find the value of $\beta$.
[1]
(d) The width of the expressway, $P S$, is 50 metres. Find the greatest and least heights of the arch, $Q R$, above the expressway.
[4]
(a) $PS$ = $2 a(\pi+\sin \beta-\beta)$
(c) $\beta=1.90$
(d) Greatest = $22.9 \mathrm{~m}$, Least = $15.1 \mathrm{~m}$
(a) $x=a(\theta-\sin \theta)$
$P S =a[(2 \pi-\beta)-\sin (2 \pi-\beta)]-a(\beta-\sin \beta) $
$=a[2 \pi-\beta-(-\sin \beta)]-a(\beta-\sin \beta) $
$=a(2 \pi-\beta+\sin \beta)-a(\beta-\sin \beta) $
$=a[(2 \pi-\beta+\sin \beta)-(\beta-\sin \beta)] $
$=a(2 \pi-\beta+\sin \beta-\beta+\sin \beta) $
$=a(2 \pi+2 \sin \beta-2 \beta) $
$=2 a(\pi+\sin \beta-\beta)$
(b)
$x =a(\theta-\sin \theta)$
$\frac{\mathrm{d} x}{\mathrm{~d} \theta} =a(1-\cos \theta)$
$\mathrm{d} x =a(1-\cos \theta) \mathrm{d} \theta$
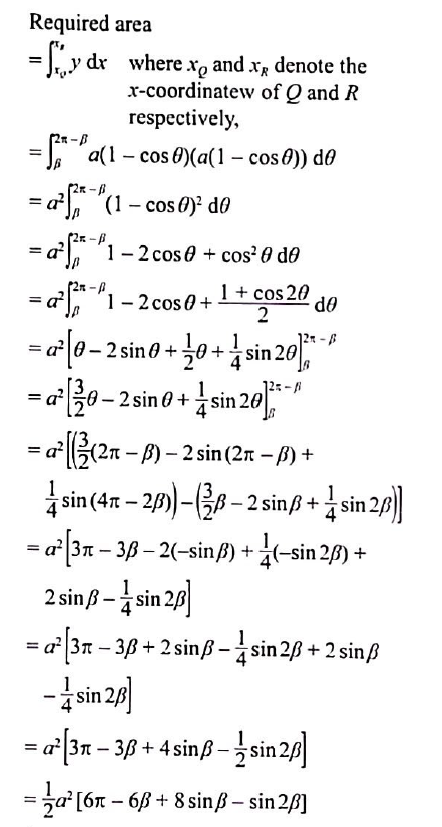
(d) $P S=50$
From (i),
$P S =2 a(\pi+\sin \beta-\beta)=50 $
$a =\frac{50}{2(\pi+\sin \beta-\beta)} \text { where } \beta=1.9000021 $
$a =11.42653444 $
$y =a(1-\cos \theta)$
Greatest height $\begin{aligned} &=a(1-\cos \pi) \ &=a(1+1) \ &=2 a \ &=2(11.42653444) \ &=22.9 \mathrm{~m} \end{aligned}$
Least height
$=a(1-\cos \beta)$
$=11.42653444(1-\cos 1.9000021)$
$=15.1 \mathrm{~m}$
This is a very tedious question. Students must know $\sin (2 \pi-\beta)=-\sin \beta$ and $\sin (4 \pi-2 \beta)=-\sin 2 \beta$ to simplify expressions and also to use a graphing calculator to solve for zero in 11 (c). The answers are not “nice” expressions and students need to do this question very carefully to arrive at the correct answers.