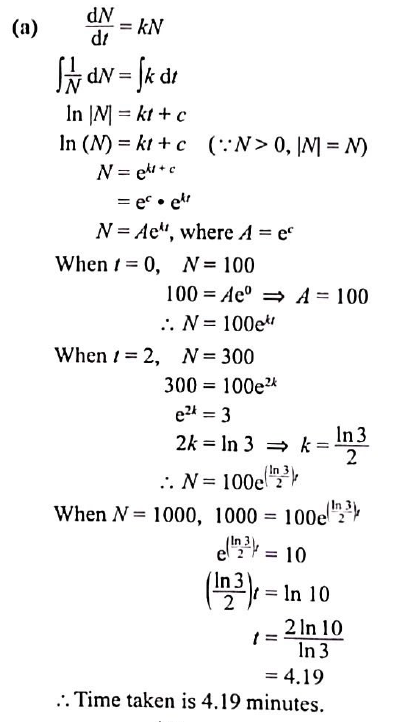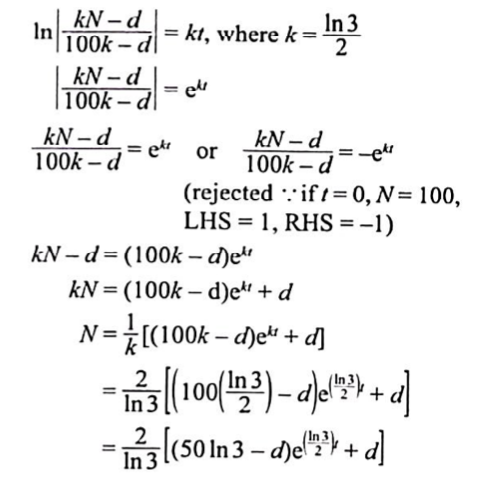Scientists model the number of bacteria, $N$, present at a time $t$ minutes after setting up an experiment. The model assumes that, at any time $t$, the growth rate in the number of bacteria is $k N$, for some positive constant $k$. Initially there are 100 bacteria and it is found that there are 300 bacteria at time $t=2$.
(a) Write down and solve a differential equation involving $N, t$ and $k$. Find $k$ and the time it takes for the number of bacteria to reach 1000 .

The scientists repeat the experiment, again with an initial number of 100 bacteria. The grouth rate, $k N$. for the number of bacteria is the same as that found in part (a). This time they add an anti-bacterial solution which they model as reducing the number of bacteria by $d$ bacteria per minute.
(b) Write down and solve a differential equation, giving $t$ in terms of $N$ and $d$. Hence find $N$ in terms of $t$ and $d$.

[5]

(c) (i) Find the range of values of $d$ for which the number of bacteria will decrease.

[1]

(ii) In the case where $d=58$, find the time taken for the number of bacteria to reach zero.

[2]