(a) $\left(\frac{\pi}{4}, \frac{1}{\sqrt{2}} e^{\frac{\pi}{4}}\right)$, Maximum point

(c) $\frac{\pi}{8}\left(\mathrm{e}^\pi-3\right)$

(a) $\mathrm{f}^{\prime}(x)=\mathrm{e}^x(-\sin x)+\cos x\left(\mathrm{e}^{\mathrm{x}}\right)$
$=\mathrm{e}^{\mathrm{x}}(\cos x-\sin x)$
For stationary point,
$\mathrm{f}^{\prime}(x)=0$
$\mathrm{e}^{\mathrm{x}}(\cos x-\sin x)=0$
Since $e^x \neq 0 \Rightarrow \cos x-\sin x=0$
$\sin x=\cos x$
$\tan x=1$
$x=\frac{\pi}{4}$

$x=\frac{\pi}{4}, \mathrm{f}\left(\frac{\pi}{4}\right)=\mathrm{e}^{\frac{\pi}{4}} \cos \frac{\pi}{4}=\frac{1}{\sqrt{2}} \mathrm{e}^{\frac{\pi}{4}}$
$\therefore$ Coordinates of stationary point of $\mathrm{f}(x)$ is
$\left(\frac{\pi}{4},\right.\left.\frac{1}{\sqrt{2}} \mathrm{e}^{\frac{\pi}{4}}\right) .$

$\mathrm{f}^{\prime \prime}(x) =\mathrm{e}^{\mathrm{r}}(-\sin x-\cos x)+(\cos x-\sin x) \mathrm{e}^r $
$=\mathrm{e}^{\mathrm{r}}(-\sin x-\cos x+\cos x-\sin x) $
$=-2 \sin x \mathrm{e}^{\mathrm{r}}$
When $x=\frac{\pi}{4}$,
$\mathrm{f}^{\prime \prime}\left(\frac{\pi}{4}\right) =-2 \sin \frac{\pi}{4} \mathrm{e}^{\frac{\pi}{4}} $
$=-2\left(\frac{\sqrt{2}}{2}\right) \mathrm{e}^{\frac{\pi}{4}} $
$=-\sqrt{2} \mathrm{e}^{\frac{\pi}{4}}<0 \quad\left(\text { since } \mathrm{e}^{\frac{\pi}{4}}>0\right)$
$\therefore\left(\frac{\pi}{4}, \frac{1}{\sqrt{2}} \mathrm{e}^{\frac{\pi}{4}}\right)$ is a maximum point.

 

(b) Let $u=\mathrm{e}^{2 \mathrm{r}} ; \quad v^{\prime}=\cos 2 \mathrm{x}$
$u^{\prime}=2 \mathrm{e}^{2 \mathrm{r}} ; \quad v=\frac{1}{2} \sin 2 x $
$\int \mathrm{e}^{2 \mathrm{r}} \cos 2 x \mathrm{dx} $
$=\left(\mathrm{e}^{2 \mathrm{r}}\right)\left(\frac{1}{2} \sin 2 x\right)-\int\left(\frac{1}{2} \sin 2x\right)\left(2 \mathrm{e}^{2 r}\right) \mathrm{dr} $
$=\frac{\mathrm{e}^{2 \mathrm{r}}}{2} \sin 2 x-\int \mathrm{e}^{2 \mathrm{r}} \sin 2 x \mathrm{~d} x $
$\text { Let } u=\mathrm{e}^{2 \mathrm{r}} ; \quad v^{\prime}=\sin 2 x $
$u^{\prime}=2 \mathrm{e}^{2 \mathrm{r}} ; \quad v=-\frac{1}{2} \cos 2 x$

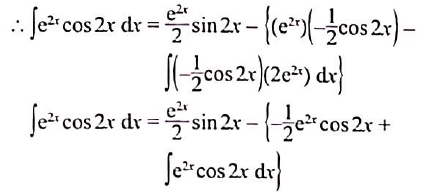
$\int \mathrm{e}^{2 x} \cos 2 x \mathrm{~d} x=\frac{\mathrm{e}^{2 x}}{2} \sin 2 x+\frac{1}{2} \mathrm{e}^{2 x} \cos 2 x-$
$\int \mathrm{e}^{2 x} \cos 2 x d x$
$2 \int \mathrm{e}^{2 x} \cos 2 x \mathrm{~d} x=\frac{\mathrm{e}^{2 x}}{2} \sin 2 x+\frac{1}{2} \mathrm{e}^{2 x} \cos 2 x+c$
$=\frac{\mathrm{e}^{2 x}}{2}(\sin 2 x+\cos 2 x)+c$
$\int \mathrm{e}^{2 \mathrm{r}} \cos 2 x \mathrm{~d} x=\frac{\mathrm{e}^{2 \mathrm{r}}}{2}(\sin 2 x+\cos 2 x)+c^{\prime}$
where $c^{\prime}=\frac{c}{2}$

 

(c) Required volume
$=\pi \int_0^{\frac{\pi}{2}} y^2 \mathrm{~d} x $
$=\pi \int_0^{\frac{\pi}{2}}\left(\mathrm{e}^x \cos x\right)^2 \mathrm{~d} x $
$=\pi \int_0^{\frac{\pi}{2}} \mathrm{e}^{2 x} \cos ^2 x \mathrm{~d} x $
$=\pi \int_0^{\frac{\pi}{2}} \frac{\mathrm{e}^{2 x}(1+\cos 2 x)}{2} \mathrm{~d} x $
$=\frac{\pi}{2} \int_0^{\frac{\pi}{2}} \mathrm{e}^{2 x}+\mathrm{e}^{2 x} \cos 2 x d x$

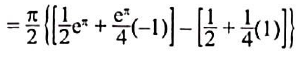
$=\frac{\pi}{2}\left[\frac{\mathrm{e}^\pi}{2}-\frac{\mathrm{e}^\pi}{4}-\frac{3}{4}\right]$
$=\frac{\pi}{2}\left[\frac{\mathrm{e}^\pi}{4}-\frac{3}{4}\right]$
$=\frac{\pi}{8}\left(\mathrm{e}^\pi-3\right)$