Question
Answer Key
Worked Solution
9758/2021/P1/Q08
The lines $l_1$ and $l_2$ have equations
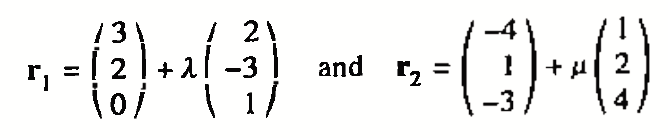
respectively, where $\lambda$ and $\mu$ are parameters.
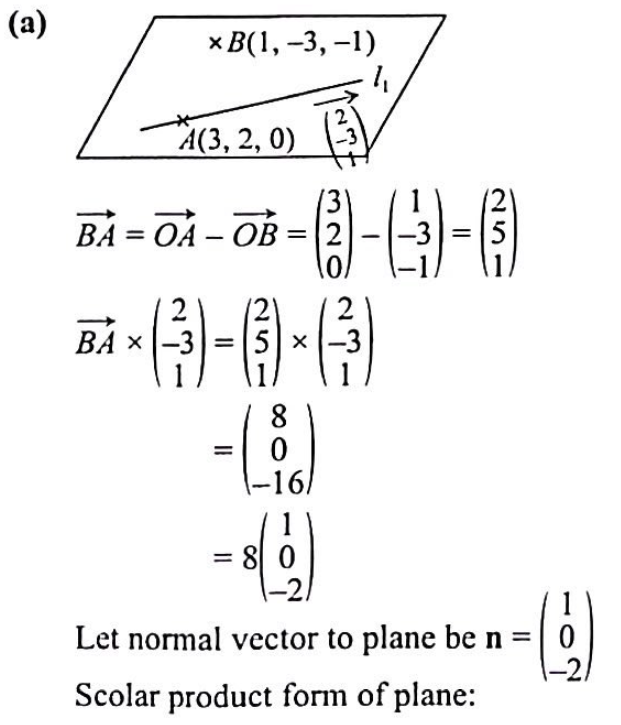
(a) Find a cartesian equation of the plane containing $l_1$ and the point $(1,-3,-1)$.
[4]
(b) Show that $l_1$ is perpendicular to $l_2$.
[2]
(c) (i) Find values of $\lambda$ and $\mu$ such that $\mathbf{r}_1-\mathbf{r}_2$ is perpendicular to both $l_1$ and $l_2$. State the position vectors of the points where the common perpendicular meets $l_1$ and $l_2$.
[6]
(ii) Find the length of this common perpendicular.
[2]
(a) $x-2 z=3$
(c) (i) $\lambda=-1$, $\mu=1$ ,
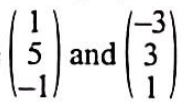
(c)(ii) $2 \sqrt{6}$

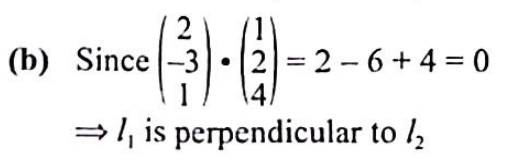
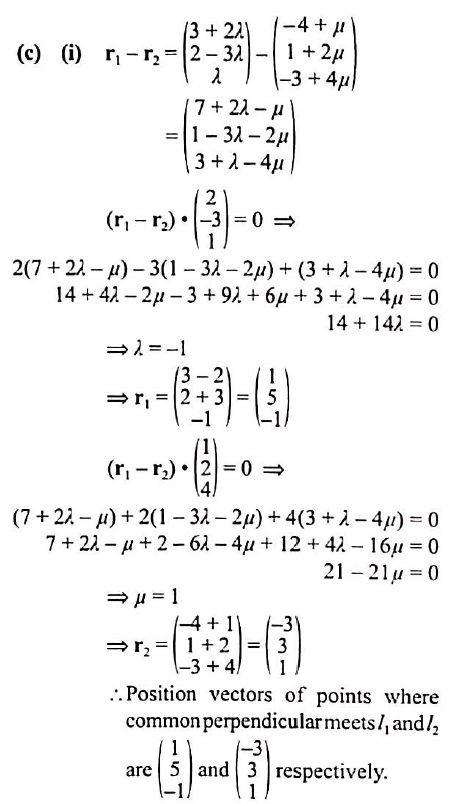
(c)
