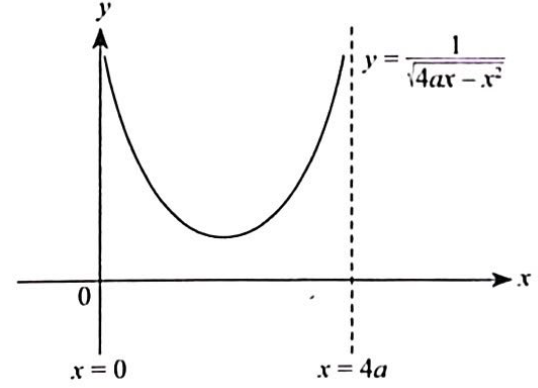
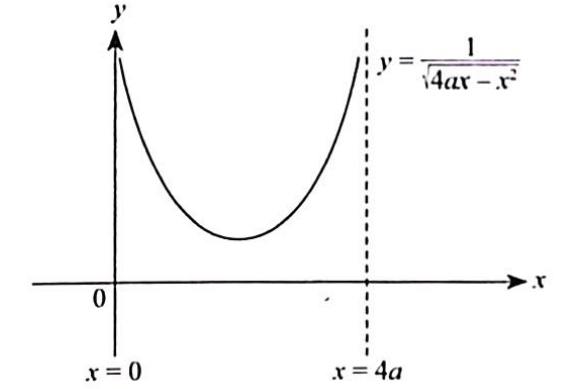
A curve $C$ has equation $y=\frac{1}{\sqrt{4 a x-x^2}}$, where $a>0$. (a) Sketch $C$ and give the equations of any asymptotes, in terms of $a$ where appropriate.
[4]
(b) Find the smallest possible value of $y$ in terms of $a$.
[1]
(c) Describe the transformation that maps the graph of $C$ onto the graph of $y=\frac{1}{\sqrt{4 a^2-x^2}}$.
[3]
(a)
(b) $\frac{1}{2 a}$
(c)The graph of $C$ is translated by $2 a$ units in the negative $x$-direction to obtain the graph of $y=\frac{1}{\sqrt{4 a^2-x^2}}$
(c) $y=\frac{1}{\sqrt{4 a x-x^2}}=\frac{1}{\sqrt{4 a^2-(x-2 a)^2}}$
The graph of $C$ is translated by $2 a$ units in the negative $x$-direction to obtain the graph of $y=\frac{1}{\sqrt{4 a^2-x^2}}$.
One has to complete the squares for the quadratic expression $4 a x-x^2$ in order to arrive at the correct transformation. This part can be challenging to some students.
(a) $\mathrm{f}(x)=y=\frac{1}{\sqrt{4 a x-x^2}}$ $\quad=\frac{1}{\sqrt{x(4 a-x)}}$ $\begin{aligned} x(4 a-x) &=0 \ \Rightarrow & \Rightarrow 0 \text { or } \quad x=4 a \end{aligned}$ $\therefore$ Vertical asymptotes: $x=0$ or $x=4 a$ For $x(4 a-x)>0$ $\Rightarrow 0<x<4 a(\therefore$ Domain of $f$ is $(0,4 a))$
(b)
$4 a x-x^2 =-\left(x^2-4 a x\right) $ $=-\left((x-2 a)^2-4 a^2\right) $ $=4 a^2-(x-2 a)^2$ Largest value of $\left(4 a x-x^2\right)$ is $4 a^2$ $\therefore$ Smallest value of $y=\frac{1}{\sqrt{4 a^2}}=\frac{1}{2 a}$
