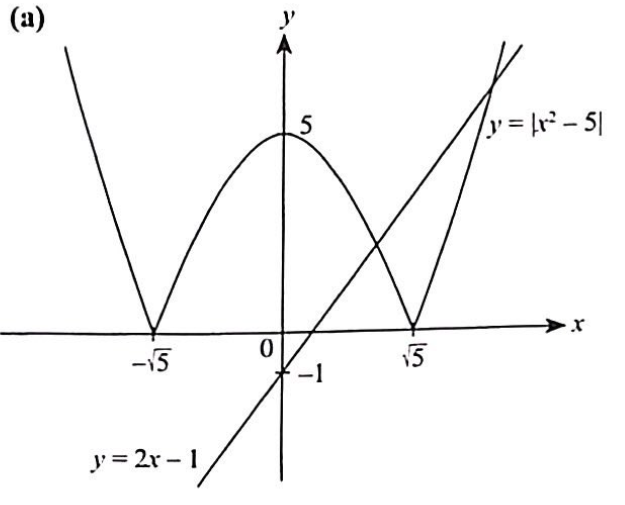
(b) $x=1+\sqrt{5}$ or $x=-1+\sqrt{7}$

$\left|x^2-5\right|=2 x-1$

$x^2-5 =2 x-1$

$x^2-2 x-4 =0$

$x =\frac{2 \pm \sqrt{(-2)^2-4(1)(-4)}}{2(1)}$

$=\frac{2 \pm \sqrt{20}}{2}$

$=\frac{2 \pm 2 \sqrt{5}}{2}$

$=1 \pm \sqrt{5}$

or

$x^2-5 =-(2 x-1)$

$x^2-5+2 x-1 =0$

$x^2+2 x-6 =0$

$x =\frac{-2 \pm \sqrt{(2)^2-4(1)(-6)}}{2(1)}$

$=\frac{-2 \pm \sqrt{28}}{2}$

$=\frac{-2 \pm 2 ; \overline{7}}{2}$

$=-1 \pm i \overline{7}$

Since $\left|x^2-5\right|=2 x-1 \geqslant 0$
$\Rightarrow x \geqslant \frac{1}{2}$
$\therefore x=1+\sqrt{5} \quad$ or $\quad x=-1+\sqrt{7}$