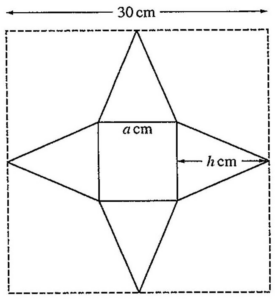
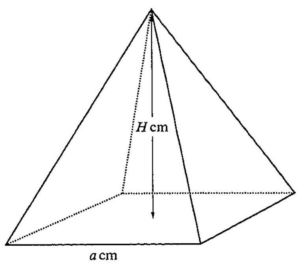
Fig. 1 shows the net of a square-based pyramid cut from a square of cardboard of side length $30 \mathrm{~cm}$. The net consists of a square of side length $a \mathrm{~cm}$ and four isosceles triangles, each with base $a \mathrm{~cm}$ and perpendicular height $h \mathrm{~cm}$. The net is folded to form a pyramid which has a square base of side length $a \mathrm{~cm}$ and vertical height $H \mathrm{~cm}$, as shown in Fig. 2.
(i) Show that $H^{2}=225-15 a$.
[2]
(ii) Find the maximum possible volume of the pyramid. You do not need to show that this value is a maximum.
[5] [The volume of a square-based pyramid is $\frac{1}{3} \times$ base area $\times$ height.]
(iii) (a) Find the value of $a$ for which the total surface area of the four triangular faces of the pyramid is a maximum. You do not need to show that this value is a maximum.
[3]
(b) Describe the shape formed from the net in this case.
(ii) $322 \mathrm{~cm}^3($ to 3 s.f.)
(iii)(a) $a=15$; (b) The net will become a square with sides $\sqrt{2} \mathrm{~cm}$
(i) By Pythagoras’ Theorem,
$$
\begin{aligned}
h^2 &=\left(\frac{a}{2}\right)^2+H^2 \\
H^2 &=h^2-\frac{a^2}{4}
\end{aligned}
$$
[M1]
Also, by observing
$$
30=a+2 h
$$
$$
\begin{aligned}
h &=\frac{30-a}{2} \\
H^2 &=\left(\frac{30-a}{2}\right)^2-\frac{a^2}{4} \\
H^2 &=\frac{(30-a)^2-a^2}{4}
\end{aligned}
$$
$$
\begin{array}{l}
H^2=\frac{900-60 a+a^2-a^2}{4} \\
H^2=225-15 a(\text { shown })
\end{array}
$$
[A1]
(ii) Volume of pyramid, $v=\frac{1}{3}(a)^2 \times H$
$$
\begin{aligned}
v &=\frac{1}{3} \times a^2 \times \sqrt{225-15 a} \\
v^2 &=\frac{a^4}{9}(225-15 a) \\
v^2 &=\frac{225}{9} a^4-\frac{15}{9} a^5
\end{aligned}
$$
[B1]
Differentiate with respect to $a$,
$$
\begin{array}{l}
2 v\left(\frac{\mathrm{d} v}{\mathrm{~d} a}\right)=\frac{900 a^3}{9}-\frac{75}{9} a^4 \\
2 v\left(\frac{\mathrm{d} v}{\mathrm{~d} a}\right)=100 a^3-\frac{25}{3} a^4
\end{array}
$$
[M1]
At stationary point,
$\frac{\mathrm{d} v}{\mathrm{~d} a}=0$
$0=100 a^3-\frac{25}{3} a^4$
$$
\begin{array}{l}
0=a^3\left(100-\frac{25}{3} a\right) \\
a^3=0 \text { or } 100-\frac{25}{3} a=0
\end{array}
$$
$a=0$ (Rejected, $a>0), a=12$
[B1]
When $a=12$,
$$
\begin{aligned}
v &=\frac{1}{3} \times 12^2 \times \sqrt{225-15(12)} \\
&=322 \mathrm{~cm}^3 \text { (to } 3 \text { s.f.) }
\end{aligned}
$$
[A1]
(iii) (a) Total surface area of the 4 triangular faces, $A$
$$
\begin{array}{l}
=\frac{1}{2} \times a \times h \times 4 \\
=2 a h \\
=2 a\left(\frac{30-a}{2}\right) [B1] \\
=a(30-a) \\
\frac{\mathrm{d} A}{\mathrm{~d} a}=30-2 a
\end{array}
$$
[M1]
At stationary point,
$\frac{\mathrm{d} A}{\mathrm{~d} a}=0$
$30-2 a=0$
$a=15$
(b) The net will become a square with sides
$\sqrt{2} \mathrm{~cm}$.
[A1]
(b) The net will become a square with sides
$$
\sqrt{2} \mathrm{~cm}
$$
[A1]