In sport science, studies are made to optimise performance in all aspects of sport from fitness to $C$ technique.

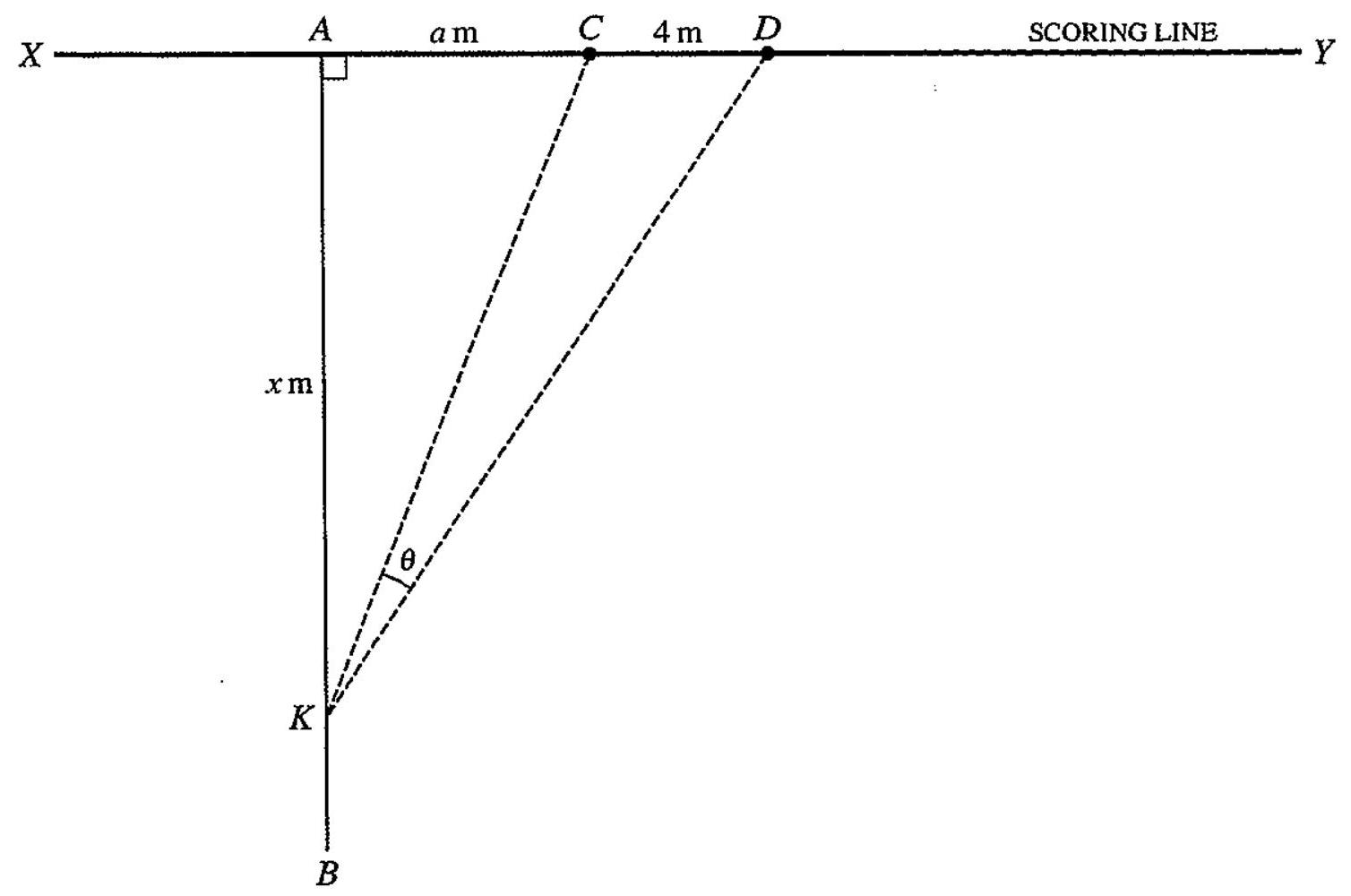
In a game, a player scores 3 points by carrying the ball over the scoring line, shown in the diagram as $X Y$. When a player has scored these 3 points, an extra point is scored if the ball is kicked between two fixed vertical posts at $C$ and $D$. The kick can be taken from any point on the line $A B$, where $A$ is the point at which the player crossed the scoring line and $A B$ is perpendicular to $X Y$.

The distance $C D$ is $4 \mathrm{~m} ; X C$ is equal to $D Y$; the point $A$ is a distance $a \mathrm{~m}$ from $C$ and $A$ lies between $X$ and $C$. The kick is taken from the point $K$, where $A K$ is $x \mathrm{~m}$. The angle $C K D$ is $\theta$ (see diagram).

(i) By expressing $\theta$ as the difference of two angles, or otherwise, show that

$$
\tan \theta=\frac{4 x}{x^{2}+4 a+a^{2}} \text {. }
$$

[3]

(ii) Find, in terms of $a$, the value of $x$ which maximises $\tan \theta$, simplifying your answer. Find also the corresponding value of $\tan \theta$. (You need not show that your answer gives a maximum.

[3]

The point corresponding to the value of $x$ found in part (ii) is called the optimal point. The corresponding value of $\theta$ is called the optimal angle.

(iii) Explain why a player may decide not to take the kick from the optimal point.

[1]

(iv) Show that, when $\theta$ is the optimal angle, $\tan K D A=\sqrt{\frac{a}{4+a}}$. Find the approximate value of angle $K D A$ when $a$ is much greater than 4 .

[3]

(v) It is given that the length of the scoring line $X Y$ is $50 \mathrm{~m}$. Find the range in which the optimal angle lies as the location of $A$ varies between $X$ and $C$.

[2]