(a) Given that $\mathbf{a}$ and $\mathbf{b}$ are non-zero vectors such that $\mathbf{a} \times \mathbf{b}=\mathbf{b} \times \mathbf{a}$, find the relationship between $\mathbf{a}$ and $\mathbf{b}$.

[2]

(b) The points $P, Q$ and $R$ have position vectors $\mathbf{p}, \mathbf{q}$ and $\mathbf{r}$ respectively. The points $P$ and $Q$ are fixed and $R$ varies.

(i) Given that $\mathbf{q}$ is non-zero and $(\mathbf{r}-\mathbf{p}) \times \mathbf{q}=\mathbf{0}$, describe geometrically the set of all possible positions of the point $R$.

[3]

(ii) Given instead that

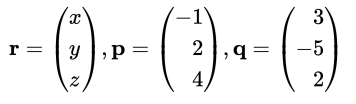
and that $(\mathbf{r}-\mathbf{p}) \cdot \mathbf{q}=0$, find the relationship between $x, y$ and $z$. Describe the set of all possible positions of the point $R$ in this case.

[4]