A company produces resistors rated at $750 \mathrm{ohms}$ for use in electronic circuits. The production manager wishes to test whether the mean resistance of these resistors is in fact $750 \mathrm{ohms}$. He knows that the resistances are normally distributed with variance $100 \mathrm{ohms}^{2}$.

(i) Explain whether the manager should carry out a 1-tail test or a 2-tail test. State hypotheses for the test, defining any symbols you use.

[2]

The production manager takes a random sample of 8 of these resistors. He finds that the resistances, in ohms, are as follows.

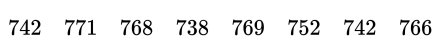
(ii) Find the mean of the sample of 8 resistors. Carry out the test, at the $5 \%$ level of significance, for the production manager. Give your conclusion in context.

[5]

The company also produces resistors rated at 1250 ohms. Nothing is known about the distribution of the resistances of these resistors.

(iii) Describe how, and why, a test of the mean resistance of the $1250 \mathrm{ohms}$ resistors would need to differ from that for the 750 ohms resistors.

[2]